| << Chapter < Page | Chapter >> Page > |
A design for a cooling tower project is shown in [link] . Find the equation of the hyperbola that models the sides of the cooling tower. Assume that the center of the hyperbola—indicated by the intersection of dashed perpendicular lines in the figure—is the origin of the coordinate plane. Round final values to four decimal places.
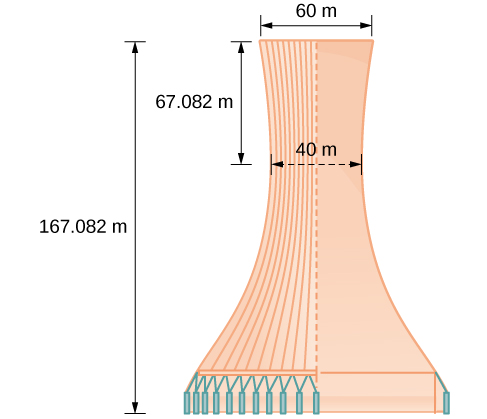
The sides of the tower can be modeled by the hyperbolic equation.
Access these online resources for additional instruction and practice with hyperbolas.
| Hyperbola, center at origin, transverse axis on x -axis | |
| Hyperbola, center at origin, transverse axis on y -axis | |
| Hyperbola, center at transverse axis parallel to x -axis | |
| Hyperbola, center at transverse axis parallel to y -axis |
Define a hyperbola in terms of its foci.
A hyperbola is the set of points in a plane the difference of whose distances from two fixed points (foci) is a positive constant.
What can we conclude about a hyperbola if its asymptotes intersect at the origin?
What must be true of the foci of a hyperbola?
The foci must lie on the transverse axis and be in the interior of the hyperbola.
If the transverse axis of a hyperbola is vertical, what do we know about the graph?
Where must the center of hyperbola be relative to its foci?
The center must be the midpoint of the line segment joining the foci.
For the following exercises, determine whether the following equations represent hyperbolas. If so, write in standard form.
For the following exercises, write the equation for the hyperbola in standard form if it is not already, and identify the vertices and foci, and write equations of asymptotes.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?