| << Chapter < Page | Chapter >> Page > |
Now, we will return to the problem posed at the beginning of the section. A bicycle ramp is constructed for high-level competition with an angle of formed by the ramp and the ground. Another ramp is to be constructed half as steep for novice competition. If for higher-level competition, what is the measurement of the angle for novice competition?
Since the angle for novice competition measures half the steepness of the angle for the high level competition, and for high competition, we can find from the right triangle and the Pythagorean theorem so that we can use the half-angle identities. See [link] .
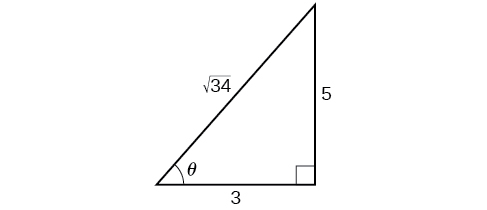
We see that We can use the half-angle formula for tangent: Since is in the first quadrant, so is
We can take the inverse tangent to find the angle: So the angle of the ramp for novice competition is
Access these online resources for additional instruction and practice with double-angle, half-angle, and reduction formulas.
| Double-angle formulas | |
| Reduction formulas | |
| Half-angle formulas |
Explain how to determine the reduction identities from the double-angle identity
Use the Pythagorean identities and isolate the squared term.
Explain how to determine the double-angle formula for using the double-angle formulas for and
We can determine the half-angle formula for by dividing the formula for by Explain how to determine two formulas for that do not involve any square roots.
multiplying the top and bottom by and respectively.
For the half-angle formula given in the previous exercise for explain why dividing by 0 is not a concern. (Hint: examine the values of necessary for the denominator to be 0.)
For the following exercises, find the exact values of a) b) and c) without solving for
If and is in quadrant I.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?