| << Chapter < Page | Chapter >> Page > |
In [link] , the quadratic was easily solved by factoring. However, there are many quadratics that cannot be factored. We can solve these quadratics by first rewriting them in standard form.
Given a quadratic function, find the intercepts by rewriting in standard form .
Find the intercepts of the quadratic function
We begin by solving for when the output will be zero.
Because the quadratic is not easily factorable in this case, we solve for the intercepts by first rewriting the quadratic in standard form.
We know that Then we solve for and
So now we can rewrite in standard form.
We can now solve for when the output will be zero.
The graph has x -intercepts at and
We can check our work by graphing the given function on a graphing utility and observing the intercepts. See [link] .
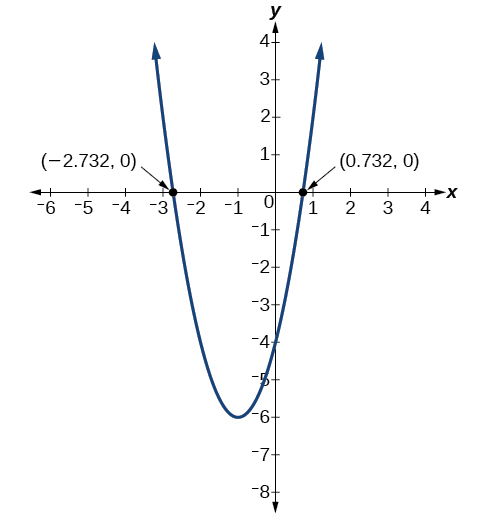
In a Try It , we found the standard and general form for the function Now find the y - and x -intercepts (if any).
y -intercept at (0, 13), No intercepts
A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation
The ball reaches a maximum height after 2.5 seconds.
The ball reaches a maximum height of 140 feet.
We use the quadratic formula.
Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.
The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds. See [link] .
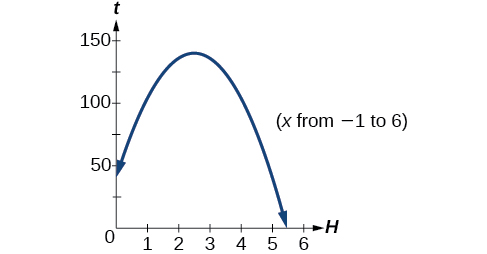
Note that the graph does not represent the physical path of the ball upward and downward. Keep the quantities on each axis in mind while interpreting the graph.
A rock is thrown upward from the top of a 112-foot high cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height above ocean can be modeled by the equation

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?