| << Chapter < Page | Chapter >> Page > |
We can also give an algebraic expression as the input to a function. For example means “first add a and b , and the result is the input for the function f .” The operations must be performed in this order to obtain the correct result.
The notation defines a function named This is read as is a function of The letter represents the input value, or independent variable. The letter or represents the output value, or dependent variable.
Use function notation to represent a function whose input is the name of a month and output is the number of days in that month.
The number of days in a month is a function of the name of the month, so if we name the function we write or The name of the month is the input to a “rule” that associates a specific number (the output) with each input.
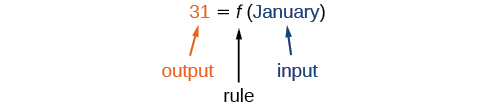
For example, because March has 31 days. The notation reminds us that the number of days, (the output), is dependent on the name of the month, (the input).
A function gives the number of police officers, in a town in year What does represent?
When we read we see that the input year is 2005. The value for the output, the number of police officers is 300. Remember, The statement tells us that in the year 2005 there were 300 police officers in the town.
Use function notation to express the weight of a pig in pounds as a function of its age in days
Instead of a notation such as could we use the same symbol for the output as for the function, such as meaning “y is a function of x?”
Yes, this is often done, especially in applied subjects that use higher math, such as physics and engineering. However, in exploring math itself we like to maintain a distinction between a function such as which is a rule or procedure, and the output we get by applying to a particular input This is why we usually use notation such as and so on.
A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases, these values represent all we know about the relationship; other times, the table provides a few select examples from a more complete relationship.
[link] lists the input number of each month (January = 1, February = 2, and so on) and the output value of the number of days in that month. This information represents all we know about the months and days for a given year (that is not a leap year). Note that, in this table, we define a days-in-a-month function where identifies months by an integer rather than by name.
| Month number, (input) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Days in month, (output) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
[link] defines a function Remember, this notation tells us that is the name of the function that takes the input and gives the output

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?