| << Chapter < Page | Chapter >> Page > |
| 1 | 2 | 3 | 4 | 5 | ||
| term of the sequence, | 2 | 4 | 8 | 16 | 32 |
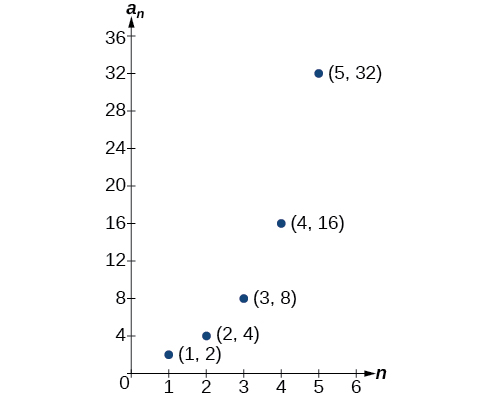
Graphing provides a visual representation of the sequence as a set of distinct points. We can see from the graph in [link] that the number of hits is rising at an exponential rate. This particular sequence forms an exponential function.
Lastly, we can write this particular sequence as
A sequence that continues indefinitely is called an infinite sequence . The domain of an infinite sequence is the set of counting numbers. If we consider only the first 10 terms of the sequence, we could write
This sequence is called a finite sequence because it does not continue indefinitely.
A sequence is a function whose domain is the set of positive integers. A finite sequence is a sequence whose domain consists of only the first positive integers. The numbers in a sequence are called terms . The variable with a number subscript is used to represent the terms in a sequence and to indicate the position of the term in the sequence.
We call the first term of the sequence, the second term of the sequence, the third term of the sequence, and so on. The term is called the term of the sequence , or the general term of the sequence. An explicit formula defines the term of a sequence using the position of the term. A sequence that continues indefinitely is an infinite sequence .
Does a sequence always have to begin with
No. In certain problems, it may be useful to define the initial term as instead of In these problems, the domain of the function includes 0.
Given an explicit formula, write the first terms of a sequence.
Write the first five terms of the sequence defined by the explicit formula
Substitute into the formula. Repeat with values 2 through 5 for
The first five terms are
Write the first five terms of the sequence defined by the explicit formula
The first five terms are
Sometimes sequences have terms that are alternate. In fact, the terms may actually alternate in sign. The steps to finding terms of the sequence are the same as if the signs did not alternate. However, the resulting terms will not show increase or decrease as increases. Let’s take a look at the following sequence.
Notice the first term is greater than the second term, the second term is less than the third term, and the third term is greater than the fourth term. This trend continues forever. Do not rearrange the terms in numerical order to interpret the sequence.
Given an explicit formula with alternating terms, write the first terms of a sequence.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?