| << Chapter < Page | Chapter >> Page > |
For the following exercises, use [link] to evaluate each trigonometric function of angle
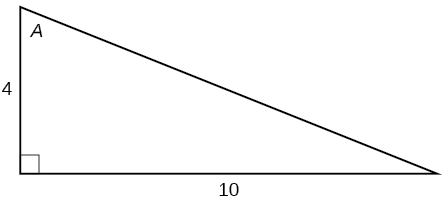
For the following exercises, use [link] to evaluate each trigonometric function of angle
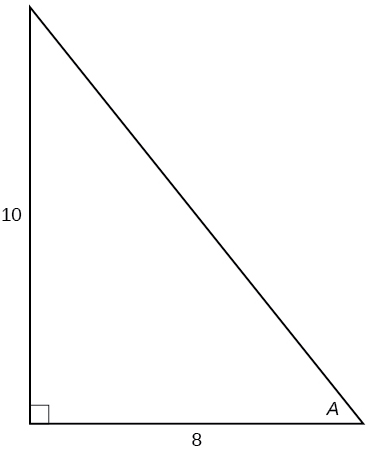
For the following exercises, solve for the unknown sides of the given triangle.
For the following exercises, use a calculator to find the length of each side to four decimal places.
A radio tower is located 400 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is and that the angle of depression to the bottom of the tower is How tall is the tower?
A radio tower is located 325 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is and that the angle of depression to the bottom of the tower is How tall is the tower?
498.3471 ft
A 200-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is and that the angle of depression to the bottom of the monument is How far is the person from the monument?
A 400-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is and that the angle of depression to the bottom of the monument is How far is the person from the monument?
1060.09 ft
There is an antenna on the top of a building. From a location 300 feet from the base of the building, the angle of elevation to the top of the building is measured to be From the same location, the angle of elevation to the top of the antenna is measured to be Find the height of the antenna.
There is lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be From the same location, the angle of elevation to the top of the lightning rod is measured to be Find the height of the lightning rod.
27.372 ft
A 33-ft ladder leans against a building so that the angle between the ground and the ladder is How high does the ladder reach up the side of the building?
A 23-ft ladder leans against a building so that the angle between the ground and the ladder is How high does the ladder reach up the side of the building?
22.6506 ft
The angle of elevation to the top of a building in New York is found to be 9 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building.
The angle of elevation to the top of a building in Seattle is found to be 2 degrees from the ground at a distance of 2 miles from the base of the building. Using this information, find the height of the building.
368.7633 ft
Assuming that a 370-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be how far from the base of the tree am I?

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?