| << Chapter < Page | Chapter >> Page > |
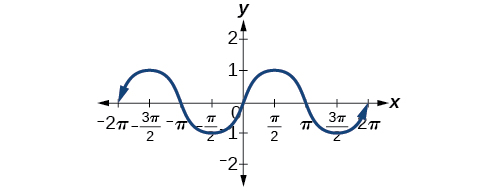
[link] shows that the cosine function is symmetric about the y -axis. Again, we determined that the cosine function is an even function. Now we can see from the graph that
The sine and cosine functions have several distinct characteristics:
As we can see, sine and cosine functions have a regular period and range. If we watch ocean waves or ripples on a pond, we will see that they resemble the sine or cosine functions. However, they are not necessarily identical. Some are taller or longer than others. A function that has the same general shape as a sine or cosine function is known as a sinusoidal function . The general forms of sinusoidal functions are
Looking at the forms of sinusoidal functions, we can see that they are transformations of the sine and cosine functions. We can use what we know about transformations to determine the period.
In the general formula, is related to the period by If then the period is less than and the function undergoes a horizontal compression, whereas if then the period is greater than and the function undergoes a horizontal stretch. For example, so the period is which we knew. If then so the period is and the graph is compressed. If then so the period is and the graph is stretched. Notice in [link] how the period is indirectly related to
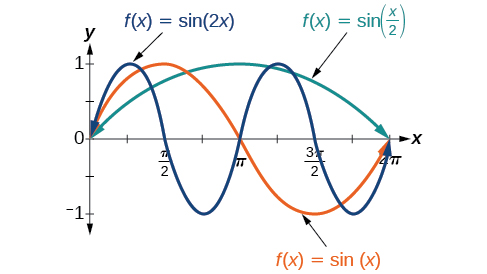
If we let and in the general form equations of the sine and cosine functions, we obtain the forms
The period is
Determine the period of the function
Let’s begin by comparing the equation to the general form
In the given equation, so the period will be
Returning to the general formula for a sinusoidal function, we have analyzed how the variable relates to the period. Now let’s turn to the variable so we can analyze how it is related to the amplitude , or greatest distance from rest. represents the vertical stretch factor, and its absolute value is the amplitude. The local maxima will be a distance above the vertical midline of the graph, which is the line because in this case, the midline is the x -axis. The local minima will be the same distance below the midline. If the function is stretched. For example, the amplitude of is twice the amplitude of If the function is compressed. [link] compares several sine functions with different amplitudes.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?