| << Chapter < Page | Chapter >> Page > |
Access these online resources for additional instruction and practice with absolute value.
How do you solve an absolute value equation?
Isolate the absolute value term so that the equation is of the form Form one equation by setting the expression inside the absolute value symbol, equal to the expression on the other side of the equation, Form a second equation by setting equal to the opposite of the expression on the other side of the equation, Solve each equation for the variable.
How can you tell whether an absolute value function has two x -intercepts without graphing the function?
When solving an absolute value function, the isolated absolute value term is equal to a negative number. What does that tell you about the graph of the absolute value function?
The graph of the absolute value function does not cross the -axis, so the graph is either completely above or completely below the -axis.
How can you use the graph of an absolute value function to determine the x -values for which the function values are negative?
Describe all numbers that are at a distance of 4 from the number 8. Express this set of numbers using absolute value notation.
Describe all numbers that are at a distance of from the number −4. Express this set of numbers using absolute value notation.
Describe the situation in which the distance that point is from 10 is at least 15 units. Express this set of numbers using absolute value notation.
Find all function values such that the distance from to the value 8 is less than 0.03 units. Express this set of numbers using absolute value notation.
For the following exercises, find the x - and y -intercepts of the graphs of each function.
For the following exercises, graph the absolute value function. Plot at least five points by hand for each graph.
For the following exercises, graph the given functions by hand.
Use a graphing utility to graph on the viewing window Identify the corresponding range. Show the graph.
range:
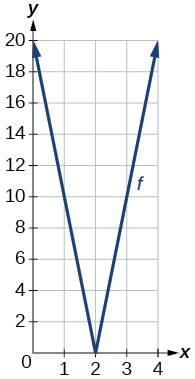
Use a graphing utility to graph on the viewing window Identify the corresponding range. Show the graph.
For the following exercises, graph each function using a graphing utility. Specify the viewing window.
For the following exercises, solve the inequality.
If possible, find all values of such that there are no intercepts for
If possible, find all values of such that there are no -intercepts for
There is no solution for that will keep the function from having a -intercept. The absolute value function always crosses the -intercept when
Cities A and B are on the same east-west line. Assume that city A is located at the origin. If the distance from city A to city B is at least 100 miles and represents the distance from city B to city A, express this using absolute value notation.
The true proportion of people who give a favorable rating to Congress is 8% with a margin of error of 1.5%. Describe this statement using an absolute value equation.
Students who score within 18 points of the number 82 will pass a particular test. Write this statement using absolute value notation and use the variable for the score.
A machinist must produce a bearing that is within 0.01 inches of the correct diameter of 5.0 inches. Using as the diameter of the bearing, write this statement using absolute value notation.
The tolerance for a ball bearing is 0.01. If the true diameter of the bearing is to be 2.0 inches and the measured value of the diameter is inches, express the tolerance using absolute value notation.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?