| << Chapter < Page | Chapter >> Page > |
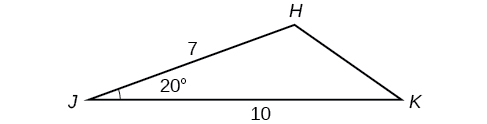
Find in [link] . Round to the nearest tenth.
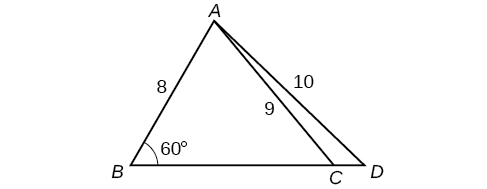
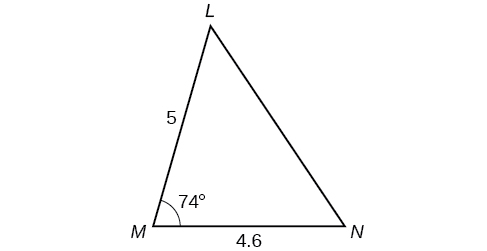
Find in [link] . Round to the nearest tenth.
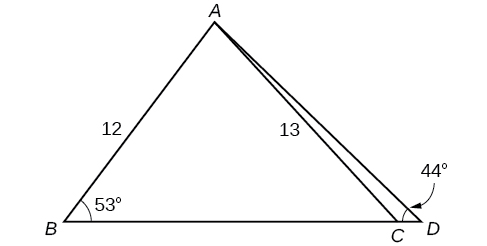
Solve both triangles in [link] . Round each answer to the nearest tenth.
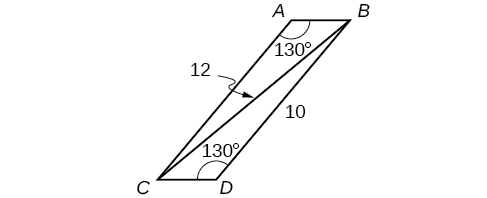
Find in the parallelogram shown in [link] .
Solve the triangle in [link] . (Hint: Draw a perpendicular from to Round each answer to the nearest tenth.
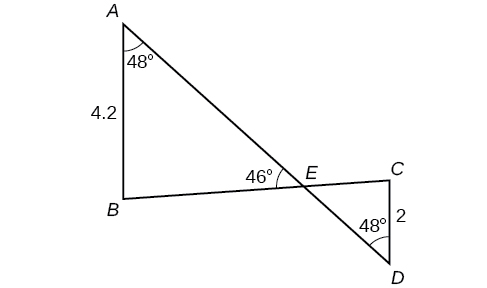
Solve the triangle in [link] . (Hint: Draw a perpendicular from to Round each answer to the nearest tenth.
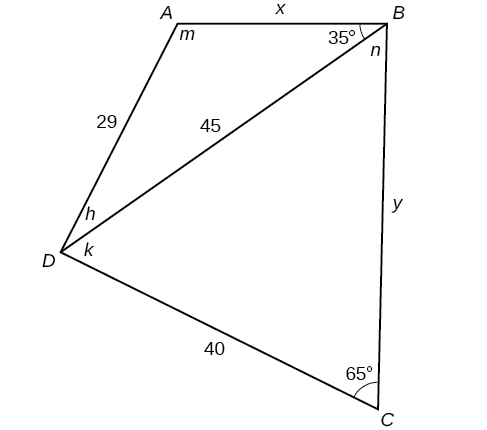
In [link] , is not a parallelogram. is obtuse. Solve both triangles. Round each answer to the nearest tenth.
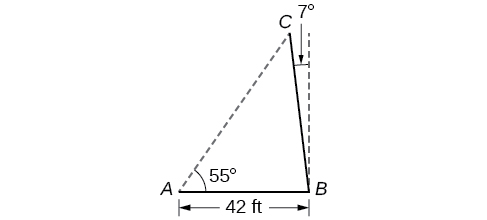
A pole leans away from the sun at an angle of to the vertical, as shown in [link] . When the elevation of the sun is the pole casts a shadow 42 feet long on the level ground. How long is the pole? Round the answer to the nearest tenth.
51.4 feet
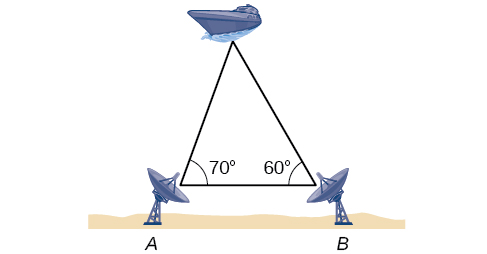
To determine how far a boat is from shore, two radar stations 500 feet apart find the angles out to the boat, as shown in [link] . Determine the distance of the boat from station and the distance of the boat from shore. Round your answers to the nearest whole foot.
[link] shows a satellite orbiting Earth. The satellite passes directly over two tracking stations and which are 69 miles apart. When the satellite is on one side of the two stations, the angles of elevation at and are measured to be and respectively. How far is the satellite from station and how high is the satellite above the ground? Round answers to the nearest whole mile.
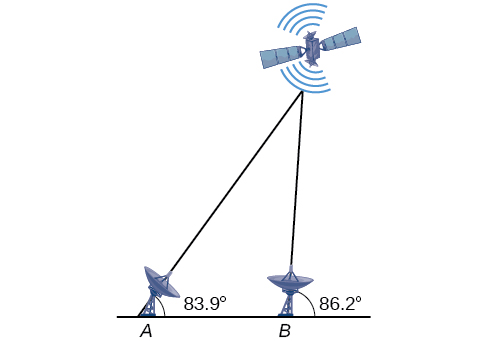
The distance from the satellite to station is approximately 1716 miles. The satellite is approximately 1706 miles above the ground.
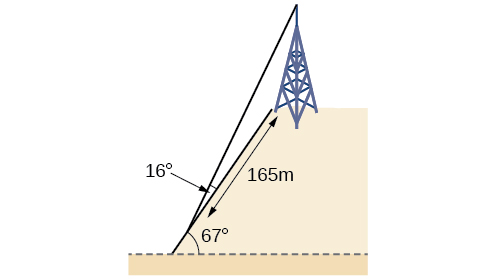
A communications tower is located at the top of a steep hill, as shown in [link] . The angle of inclination of the hill is A guy wire is to be attached to the top of the tower and to the ground, 165 meters downhill from the base of the tower. The angle formed by the guy wire and the hill is Find the length of the cable required for the guy wire to the nearest whole meter.
The roof of a house is at a angle. An 8-foot solar panel is to be mounted on the roof and should be angled relative to the horizontal for optimal results. (See [link] ). How long does the vertical support holding up the back of the panel need to be? Round to the nearest tenth.
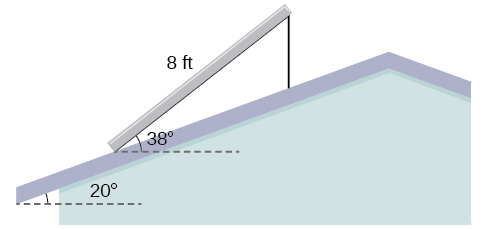
2.6 ft
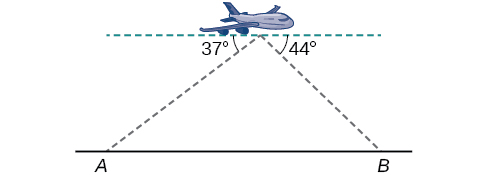
Similar to an angle of elevation, an angle of depression is the acute angle formed by a horizontal line and an observer’s line of sight to an object below the horizontal. A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 6.6 km apart, to be and as shown in [link] . Find the distance of the plane from point to the nearest tenth of a kilometer.
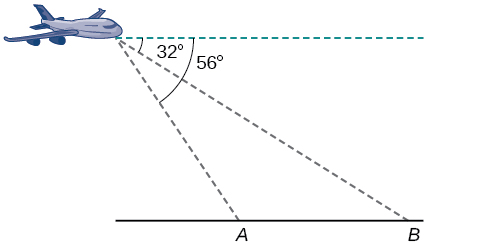
A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 4.3 km apart, to be 32° and 56°, as shown in [link] . Find the distance of the plane from point to the nearest tenth of a kilometer.
5.6 km
In order to estimate the height of a building, two students stand at a certain distance from the building at street level. From this point, they find the angle of elevation from the street to the top of the building to be 39°. They then move 300 feet closer to the building and find the angle of elevation to be 50°. Assuming that the street is level, estimate the height of the building to the nearest foot.
In order to estimate the height of a building, two students stand at a certain distance from the building at street level. From this point, they find the angle of elevation from the street to the top of the building to be 35°. They then move 250 feet closer to the building and find the angle of elevation to be 53°. Assuming that the street is level, estimate the height of the building to the nearest foot.
371 ft
Points and are on opposite sides of a lake. Point is 97 meters from The measure of angle is determined to be 101°, and the measure of angle is determined to be 53°. What is the distance from to rounded to the nearest whole meter?
A man and a woman standing miles apart spot a hot air balloon at the same time. If the angle of elevation from the man to the balloon is 27°, and the angle of elevation from the woman to the balloon is 41°, find the altitude of the balloon to the nearest foot.
5936 ft
Two search teams spot a stranded climber on a mountain. The first search team is 0.5 miles from the second search team, and both teams are at an altitude of 1 mile. The angle of elevation from the first search team to the stranded climber is 15°. The angle of elevation from the second search team to the climber is 22°. What is the altitude of the climber? Round to the nearest tenth of a mile.
A street light is mounted on a pole. A 6-foot-tall man is standing on the street a short distance from the pole, casting a shadow. The angle of elevation from the tip of the man’s shadow to the top of his head of 28°. A 6-foot-tall woman is standing on the same street on the opposite side of the pole from the man. The angle of elevation from the tip of her shadow to the top of her head is 28°. If the man and woman are 20 feet apart, how far is the street light from the tip of the shadow of each person? Round the distance to the nearest tenth of a foot.
24.1 ft
Three cities, and are located so that city is due east of city If city is located 35° west of north from city and is 100 miles from city and 70 miles from city how far is city from city Round the distance to the nearest tenth of a mile.
Two streets meet at an 80° angle. At the corner, a park is being built in the shape of a triangle. Find the area of the park if, along one road, the park measures 180 feet, and along the other road, the park measures 215 feet.
19,056 ft 2
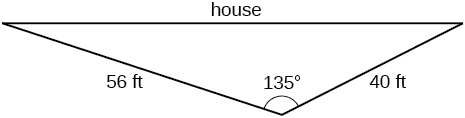
Brian’s house is on a corner lot. Find the area of the front yard if the edges measure 40 and 56 feet, as shown in [link] .
The Bermuda triangle is a region of the Atlantic Ocean that connects Bermuda, Florida, and Puerto Rico. Find the area of the Bermuda triangle if the distance from Florida to Bermuda is 1030 miles, the distance from Puerto Rico to Bermuda is 980 miles, and the angle created by the two distances is 62°.
445,624 square miles
A yield sign measures 30 inches on all three sides. What is the area of the sign?
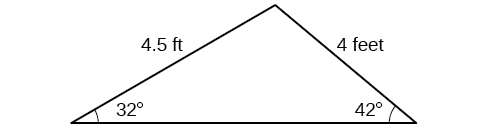
Naomi bought a modern dining table whose top is in the shape of a triangle. Find the area of the table top if two of the sides measure 4 feet and 4.5 feet, and the smaller angles measure 32° and 42°, as shown in [link] .
8.65 ft 2

Notification Switch
Would you like to follow the 'Contemporary math applications' conversation and receive update notifications?