| << Chapter < Page | Chapter >> Page > |
For the following exercises, evaluate each root.
Evaluate the cube root of when
For the following exercises, plot the complex number in the complex plane.
For the following exercises, eliminate the parameter to rewrite the parametric equation as a Cartesian equation.
Parameterize (write a parametric equation for) each Cartesian equation by using and for
Parameterize the line from to so that the line is at at and at
For the following exercises, make a table of values for each set of parametric equations, graph the equations, and include an orientation; then write the Cartesian equation.
A ball is launched with an initial velocity of 80 feet per second at an angle of 40° to the horizontal. The ball is released at a height of 4 feet above the ground.
For the following exercises, determine whether the two vectors, and are equal, where has an initial point and a terminal point and has an initial point and a terminal point
For the following exercises, use the vectors and to evaluate the expression.
For the following exercises, find a unit vector in the same direction as the given vector.
a = 8 i − 6 j
For the following exercises, find the magnitude and direction of the vector.
For the following exercises, calculate
u = −2 i + j and v = 3 i + 7 j
Given v draw v , 2 v , and v .
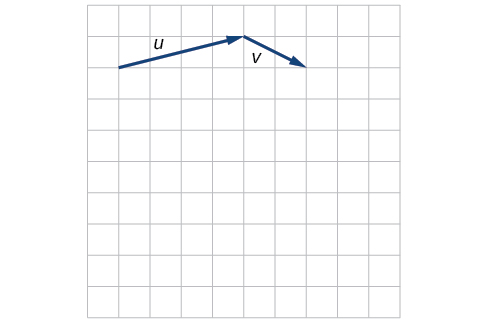
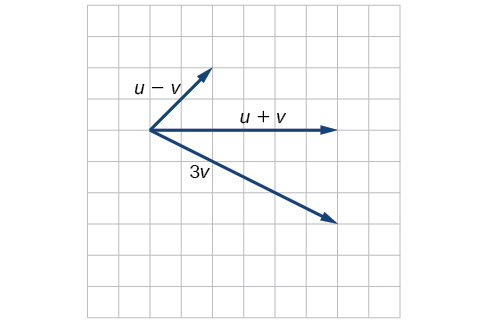
Given the vectors shown in [link] , sketch u + v , u − v and 3 v .
Given initial point and terminal point write the vector in terms of and Draw the points and the vector on the graph.
Assume is opposite side is opposite side and is opposite side Solve the triangle, if possible, and round each answer to the nearest tenth, given
Find the area of the triangle in [link] . Round each answer to the nearest tenth.

A pilot flies in a straight path for 2 hours. He then makes a course correction, heading 15° to the right of his original course, and flies 1 hour in the new direction. If he maintains a constant speed of 575 miles per hour, how far is he from his starting position?
Convert to polar coordinates, and then plot the point.
Convert the polar equation to a Cartesian equation:
Test the equation for symmetry:
Write the complex number in polar form:
Given and evaluate each expression.
Plot the complex number in the complex plane.
Eliminate the parameter to rewrite the following parametric equations as a Cartesian equation:
Parameterize (write a parametric equation for) the following Cartesian equation by using and
Graph the set of parametric equations and find the Cartesian equation:

A ball is launched with an initial velocity of 95 feet per second at an angle of 52° to the horizontal. The ball is released at a height of 3.5 feet above the ground.
For the following exercises, use the vectors u = i − 3 j and v = 2 i + 3 j .
Calculate
Given vector has an initial point and terminal point write the vector in terms of and On the graph, draw and

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?