| << Chapter < Page | Chapter >> Page > |
Should I draw diagrams when given information based on a geometric shape?
Yes. Sketch the figure and label the quantities and unknowns on the sketch.
There is a straight road leading from the town of Westborough to Agritown 30 miles east and 10 miles north. Partway down this road, it junctions with a second road, perpendicular to the first, leading to the town of Eastborough. If the town of Eastborough is located 20 miles directly east of the town of Westborough, how far is the road junction from Westborough?
It might help here to draw a picture of the situation. See [link] . It would then be helpful to introduce a coordinate system. While we could place the origin anywhere, placing it at Westborough seems convenient. This puts Agritown at coordinates and Eastborough at
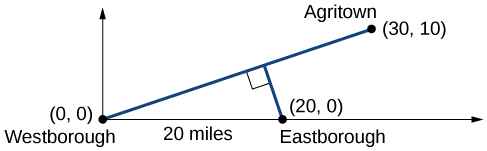
Using this point along with the origin, we can find the slope of the line from Westborough to Agritown.
Now we can write an equation to describe the road from Westborough to Agritown.
From this, we can determine the perpendicular road to Eastborough will have slope Because the town of Eastborough is at the point (20, 0), we can find the equation.
We can now find the coordinates of the junction of the roads by finding the intersection of these lines. Setting them equal,
The roads intersect at the point (18, 6). Using the distance formula, we can now find the distance from Westborough to the junction.
There is a straight road leading from the town of Timpson to Ashburn 60 miles east and 12 miles north. Partway down the road, it junctions with a second road, perpendicular to the first, leading to the town of Garrison. If the town of Garrison is located 22 miles directly east of the town of Timpson, how far is the road junction from Timpson?
21.15 miles
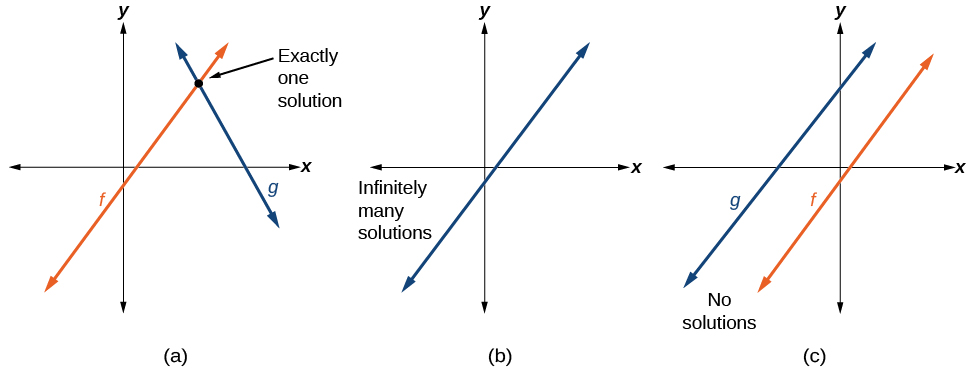
Real-world situations including two or more linear functions may be modeled with a system of linear equations . Remember, when solving a system of linear equations, we are looking for points the two lines have in common. Typically, there are three types of answers possible, as shown in [link] .
Given a situation that represents a system of linear equations, write the system of equations and identify the solution.
Jamal is choosing between two truck-rental companies. The first, Keep on Trucking, Inc., charges an up-front fee of $20, then 59 cents a mile. The second, Move It Your Way, charges an up-front fee of $16, then 63 cents a mile Rates retrieved Aug 2, 2010 from http://www.budgettruck.com and http://www.uhaul.com/ . When will Keep on Trucking, Inc. be the better choice for Jamal?
The two important quantities in this problem are the cost and the number of miles driven. Because we have two companies to consider, we will define two functions in [link] .
| Input | distance driven in miles |
| Outputs |
cost, in dollars, for renting from Keep on Trucking cost, in dollars, for renting from Move It Your Way |
| Initial Value | Up-front fee: and |
| Rate of Change | /mile and /mile |
A linear function is of the form Using the rates of change and initial charges, we can write the equations
Using these equations, we can determine when Keep on Trucking, Inc., will be the better choice. Because all we have to make that decision from is the costs, we are looking for when Move It Your Way, will cost less, or when The solution pathway will lead us to find the equations for the two functions, find the intersection, and then see where the function is smaller.
These graphs are sketched in [link] , with in blue.
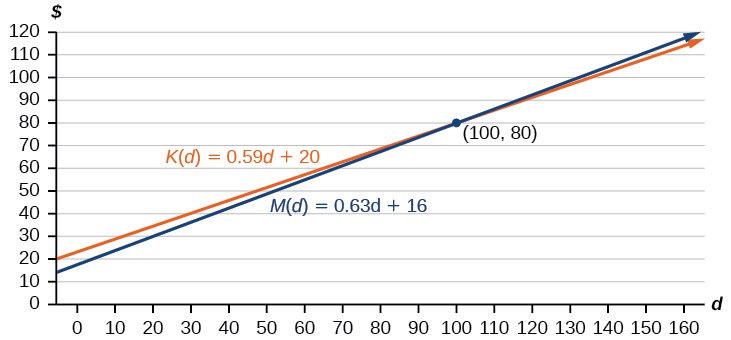
To find the intersection, we set the equations equal and solve:
This tells us that the cost from the two companies will be the same if 100 miles are driven. Either by looking at the graph, or noting that is growing at a slower rate, we can conclude that Keep on Trucking, Inc. will be the cheaper price when more than 100 miles are driven, that is .

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?