| << Chapter < Page | Chapter >> Page > |
Could we have substituted values for into the second equation to solve for in [link] ?
Yes, but because is squared in the second equation this could give us extraneous solutions for
For
This gives us the same value as in the solution.
For
Notice that is an extraneous solution.
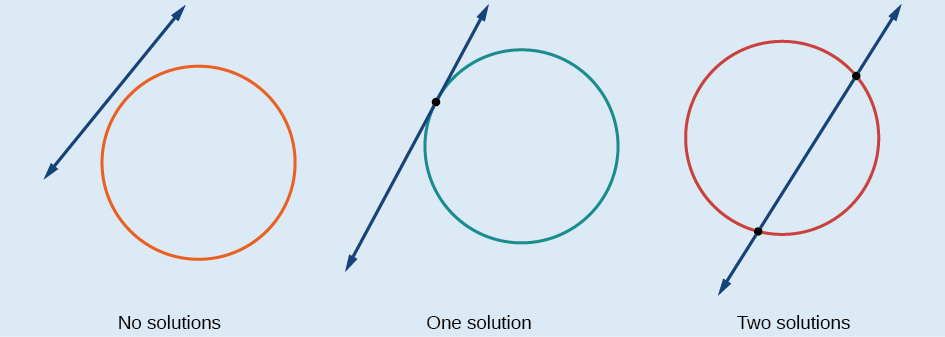
Just as with a parabola and a line, there are three possible outcomes when solving a system of equations representing a circle and a line.
[link] illustrates possible solution sets for a system of equations involving a circle and a line.
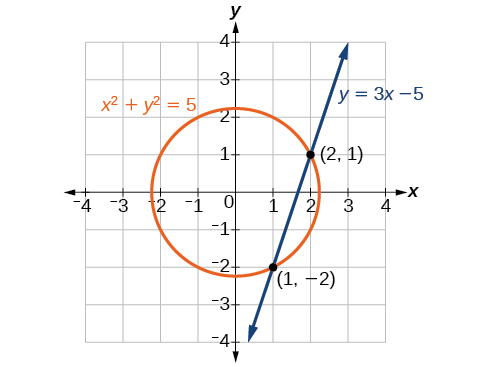
Given a system of equations containing a line and a circle, find the solution.
Find the intersection of the given circle and the given line by substitution.
One of the equations has already been solved for We will substitute into the equation for the circle.
Now, we factor and solve for
Substitute the two x -values into the original linear equation to solve for
The line intersects the circle at and which can be verified by substituting these values into both of the original equations. See [link] .
We have seen that substitution is often the preferred method when a system of equations includes a linear equation and a nonlinear equation. However, when both equations in the system have like variables of the second degree, solving them using elimination by addition is often easier than substitution. Generally, elimination is a far simpler method when the system involves only two equations in two variables (a two-by-two system), rather than a three-by-three system, as there are fewer steps. As an example, we will investigate the possible types of solutions when solving a system of equations representing a circle and an ellipse.
[link] illustrates possible solution sets for a system of equations involving a circle and an ellipse .


Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?