| << Chapter < Page | Chapter >> Page > |
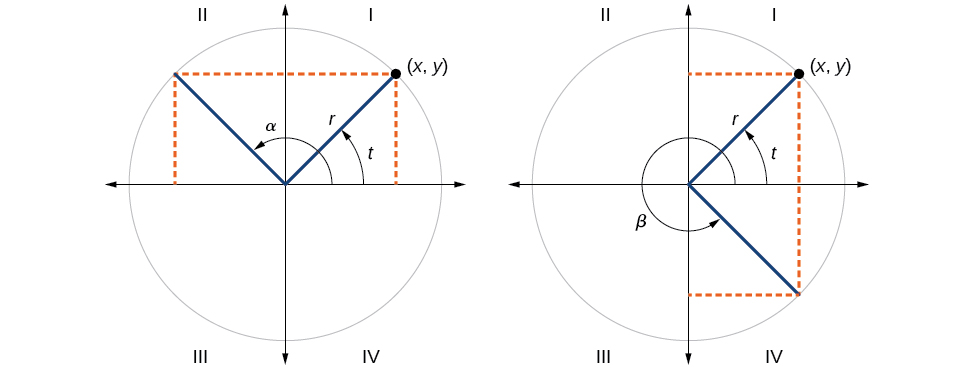
Likewise, there will be an angle in the fourth quadrant with the same cosine as the original angle. The angle with the same cosine will share the same x -value but will have the opposite y -value. Therefore, its sine value will be the opposite of the original angle’s sine value.
As shown in [link] , angle has the same sine value as angle the cosine values are opposites. Angle has the same cosine value as angle the sine values are opposites.
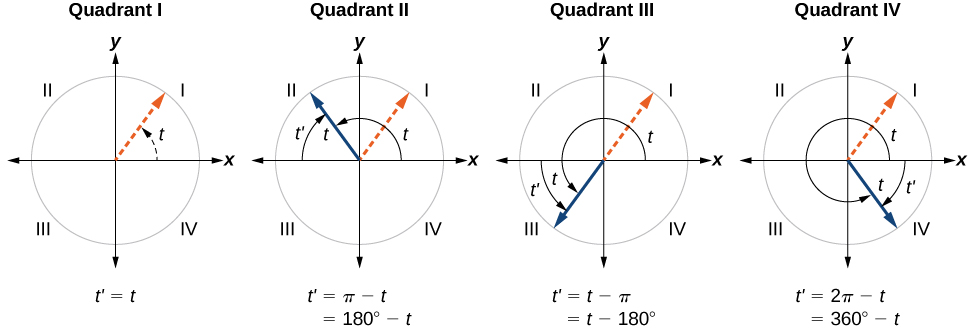
Recall that an angle’s reference angle is the acute angle, formed by the terminal side of the angle and the horizontal axis. A reference angle is always an angle between and or and radians. As we can see from [link] , for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.
Given an angle between and find its reference angle.
Because is in the third quadrant, the reference angle is
Now let’s take a moment to reconsider the Ferris wheel introduced at the beginning of this section. Suppose a rider snaps a photograph while stopped twenty feet above ground level. The rider then rotates three-quarters of the way around the circle. What is the rider’s new elevation? To answer questions such as this one, we need to evaluate the sine or cosine functions at angles that are greater than 90 degrees or at a negative angle. Reference angles make it possible to evaluate trigonometric functions for angles outside the first quadrant. They can also be used to find coordinates for those angles. We will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the angle lies.
We can find the cosine and sine of any angle in any quadrant if we know the cosine or sine of its reference angle. The absolute values of the cosine and sine of an angle are the same as those of the reference angle. The sign depends on the quadrant of the original angle. The cosine will be positive or negative depending on the sign of the x -values in that quadrant. The sine will be positive or negative depending on the sign of the y -values in that quadrant.
Angles have cosines and sines with the same absolute value as their reference angles. The sign (positive or negative) can be determined from the quadrant of the angle.
Given an angle in standard position, find the reference angle, and the cosine and sine of the original angle.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?