| << Chapter < Page | Chapter >> Page > |
The standard form of a quadratic function presents the function in the form
where is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function .
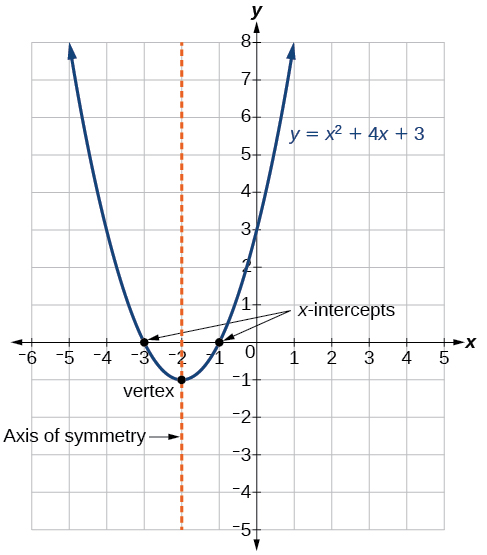
As with the general form, if the parabola opens upward and the vertex is a minimum. If the parabola opens downward, and the vertex is a maximum. [link] represents the graph of the quadratic function written in standard form as Since in this example, In this form, and Because the parabola opens downward. The vertex is at
The standard form is useful for determining how the graph is transformed from the graph of [link] is the graph of this basic function.
If the graph shifts upward, whereas if the graph shifts downward. In [link] , so the graph is shifted 4 units upward. If the graph shifts toward the right and if the graph shifts to the left. In [link] , so the graph is shifted 2 units to the left. The magnitude of indicates the stretch of the graph. If the point associated with a particular value shifts farther from the x- axis, so the graph appears to become narrower, and there is a vertical stretch. But if the point associated with a particular value shifts closer to the x- axis, so the graph appears to become wider, but in fact there is a vertical compression. In [link] , so the graph becomes narrower.
The standard form and the general form are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the standard form.
For the linear terms to be equal, the coefficients must be equal.
This is the axis of symmetry we defined earlier. Setting the constant terms equal:
In practice, though, it is usually easier to remember that k is the output value of the function when the input is so
A quadratic function is a polynomial function of degree two. The graph of a quadratic function is a parabola.
The general form of a quadratic function is where and are real numbers and
The standard form of a quadratic function is where
The vertex is located at
Given a graph of a quadratic function, write the equation of the function in general form.
Write an equation for the quadratic function in [link] as a transformation of and then expand the formula, and simplify terms to write the equation in general form.
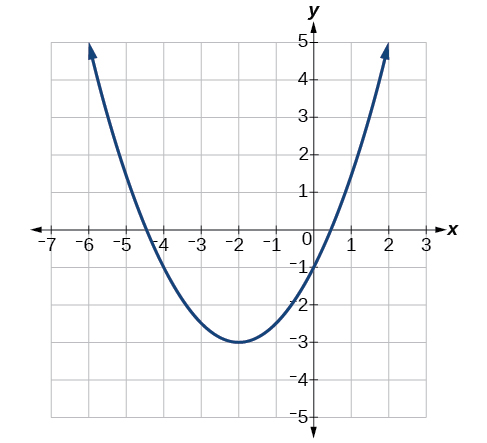
We can see the graph of g is the graph of shifted to the left 2 and down 3, giving a formula in the form
Substituting the coordinates of a point on the curve, such as we can solve for the stretch factor.
In standard form, the algebraic model for this graph is
To write this in general polynomial form, we can expand the formula and simplify terms.
Notice that the horizontal and vertical shifts of the basic graph of the quadratic function determine the location of the vertex of the parabola; the vertex is unaffected by stretches and compressions.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?