| << Chapter < Page | Chapter >> Page > |
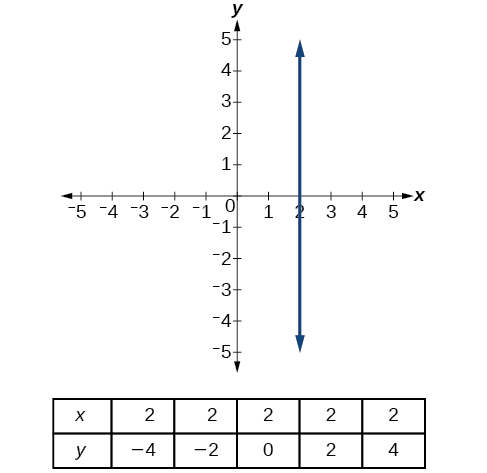
A vertical line indicates a constant input, or x -value. We can see that the input value for every point on the line is 2, but the output value varies. Because this input value is mapped to more than one output value, a vertical line does not represent a function. Notice that between any two points, the change in the input values is zero. In the slope formula, the denominator will be zero, so the slope of a vertical line is undefined.
A vertical line, such as the one in [link] , has an x -intercept, but no y- intercept unless it’s the line This graph represents the line
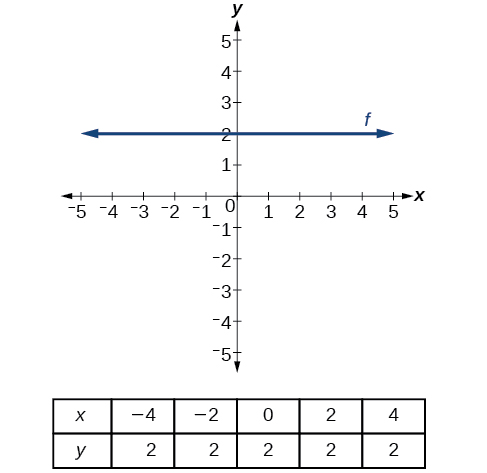
Lines can be horizontal or vertical.
A horizontal line is a line defined by an equation in the form
A vertical line is a line defined by an equation in the form
For any x -value, the y -value is so the equation is
The constant x -value is so the equation is
The two lines in [link] are parallel lines : they will never intersect. They have exactly the same steepness, which means their slopes are identical. The only difference between the two lines is the y -intercept. If we shifted one line vertically toward the other, they would become coincident.
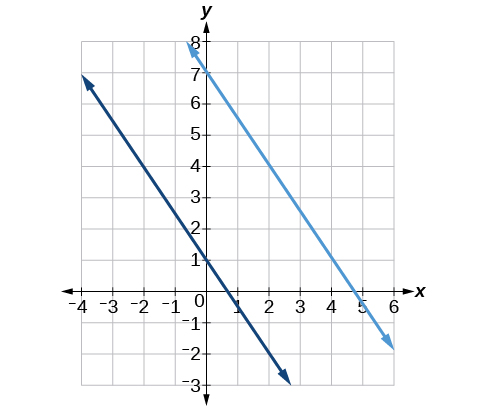
We can determine from their equations whether two lines are parallel by comparing their slopes. If the slopes are the same and the y -intercepts are different, the lines are parallel. If the slopes are different, the lines are not parallel.
Unlike parallel lines, perpendicular lines do intersect. Their intersection forms a right, or 90-degree, angle. The two lines in [link] are perpendicular.
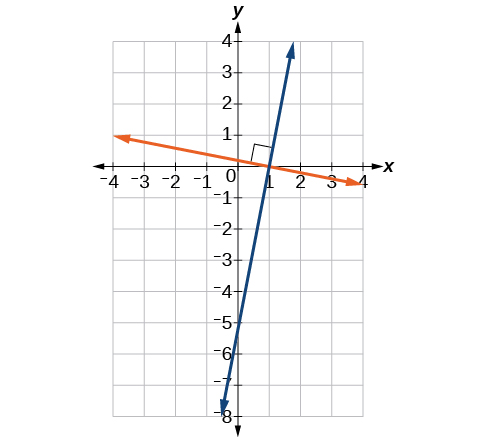
Perpendicular lines do not have the same slope. The slopes of perpendicular lines are different from one another in a specific way. The slope of one line is the negative reciprocal of the slope of the other line. The product of a number and its reciprocal is So, if are negative reciprocals of one another, they can be multiplied together to yield
To find the reciprocal of a number, divide 1 by the number. So the reciprocal of 8 is and the reciprocal of is 8. To find the negative reciprocal, first find the reciprocal and then change the sign.
As with parallel lines, we can determine whether two lines are perpendicular by comparing their slopes, assuming that the lines are neither horizontal nor vertical. The slope of each line below is the negative reciprocal of the other so the lines are perpendicular.
The product of the slopes is –1.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?