| << Chapter < Page | Chapter >> Page > |
A couple decides to start a college fund for their daughter. They plan to invest $50 in the fund each month. The fund pays 6% annual interest, compounded monthly. How much money will they have saved when their daughter is ready to start college in 6 years? In this section, we will learn how to answer this question. To do so, we need to consider the amount of money invested and the amount of interest earned.
To find the total amount of money in the college fund and the sum of the amounts deposited, we need to add the amounts deposited each month and the amounts earned monthly. The sum of the terms of a sequence is called a series . Consider, for example, the following series.
The partial sum of a series is the sum of a finite number of consecutive terms beginning with the first term. The notation represents the partial sum.
Summation notation is used to represent series. Summation notation is often known as sigma notation because it uses the Greek capital letter sigma , to represent the sum. Summation notation includes an explicit formula and specifies the first and last terms in the series. An explicit formula for each term of the series is given to the right of the sigma. A variable called the index of summation is written below the sigma. The index of summation is set equal to the lower limit of summation , which is the number used to generate the first term in the series. The number above the sigma, called the upper limit of summation , is the number used to generate the last term in a series.
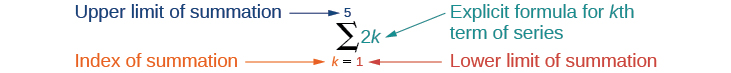
If we interpret the given notation, we see that it asks us to find the sum of the terms in the series for through We can begin by substituting the terms for and listing out the terms of this series.
We can find the sum of the series by adding the terms:
The sum of the first terms of a series can be expressed in summation notation as follows:
This notation tells us to find the sum of from to
is called the index of summation , 1 is the lower limit of summation , and is the upper limit of summation .
Does the lower limit of summation have to be 1?
No. The lower limit of summation can be any number, but 1 is frequently used. We will look at examples with lower limits of summation other than 1.
Given summation notation for a series, evaluate the value.
Evaluate
According to the notation, the lower limit of summation is 3 and the upper limit is 7. So we need to find the sum of from to We find the terms of the series by substituting and into the function We add the terms to find the sum.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?