| << Chapter < Page | Chapter >> Page > |
Identify the graph of each of the following nondegenerate conic sections.

and so we observe that and have opposite signs. The graph of this equation is a hyperbola.
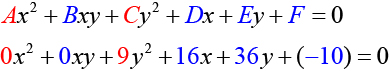
and We can determine that the equation is a parabola, since is zero.

and Because the graph of this equation is a circle.
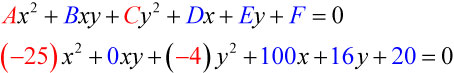
and Because and the graph of this equation is an ellipse.
Identify the graph of each of the following nondegenerate conic sections.
Until now, we have looked at equations of conic sections without an term, which aligns the graphs with the x - and y -axes. When we add an term, we are rotating the conic about the origin. If the x - and y -axes are rotated through an angle, say then every point on the plane may be thought of as having two representations: on the Cartesian plane with the original x -axis and y -axis, and on the new plane defined by the new, rotated axes, called the x' -axis and y' -axis. See [link] .

We will find the relationships between and on the Cartesian plane with and on the new rotated plane. See [link] .

The original coordinate x - and y -axes have unit vectors and The rotated coordinate axes have unit vectors and The angle is known as the angle of rotation . See [link] . We may write the new unit vectors in terms of the original ones.

Consider a vector in the new coordinate plane. It may be represented in terms of its coordinate axes.
Because we have representations of and in terms of the new coordinate system.
If a point on the Cartesian plane is represented on a new coordinate plane where the axes of rotation are formed by rotating an angle from the positive x -axis, then the coordinates of the point with respect to the new axes are We can use the following equations of rotation to define the relationship between and
and
Given the equation of a conic, find a new representation after rotating through an angle.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?