| << Chapter < Page | Chapter >> Page > |
Solve the triangle shown in [link] to the nearest tenth.
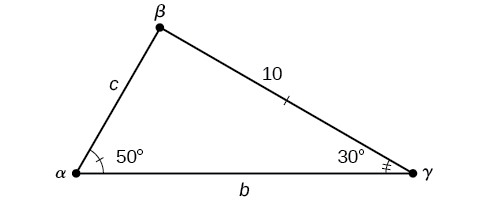
The three angles must add up to 180 degrees. From this, we can determine that
To find an unknown side, we need to know the corresponding angle and a known ratio. We know that angle and its corresponding side We can use the following proportion from the Law of Sines to find the length of
Similarly, to solve for we set up another proportion.
Therefore, the complete set of angles and sides is
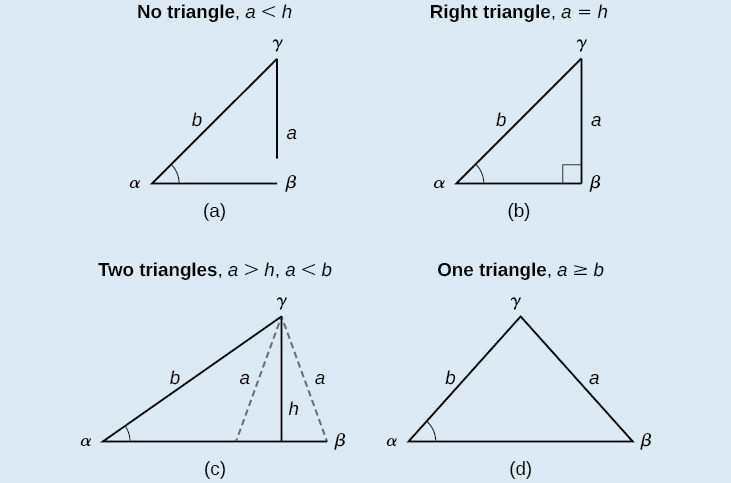
We can use the Law of Sines to solve any oblique triangle, but some solutions may not be straightforward. In some cases, more than one triangle may satisfy the given criteria, which we describe as an ambiguous case . Triangles classified as SSA, those in which we know the lengths of two sides and the measurement of the angle opposite one of the given sides, may result in one or two solutions, or even no solution.
Oblique triangles in the category SSA may have four different outcomes. [link] illustrates the solutions with the known sides and and known angle
Solve the triangle in [link] for the missing side and find the missing angle measures to the nearest tenth.
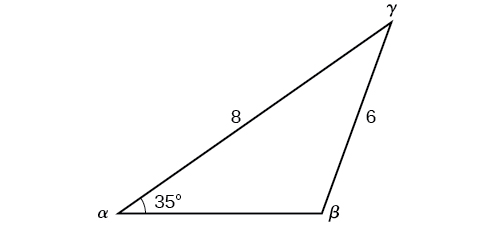
Use the Law of Sines to find angle and angle and then side Solving for we have the proportion
However, in the diagram, angle appears to be an obtuse angle and may be greater than 90°. How did we get an acute angle, and how do we find the measurement of Let’s investigate further. Dropping a perpendicular from and viewing the triangle from a right angle perspective, we have [link] . It appears that there may be a second triangle that will fit the given criteria.
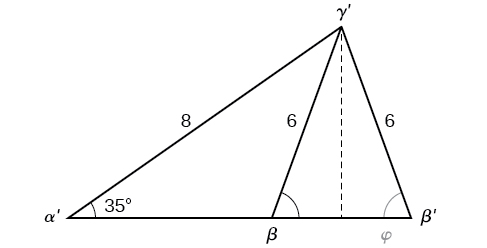
The angle supplementary to is approximately equal to 49.9°, which means that (Remember that the sine function is positive in both the first and second quadrants.) Solving for we have
We can then use these measurements to solve the other triangle. Since is supplementary to the sum of and we have
Now we need to find and
We have
Finally,
To summarize, there are two triangles with an angle of 35°, an adjacent side of 8, and an opposite side of 6, as shown in [link] .
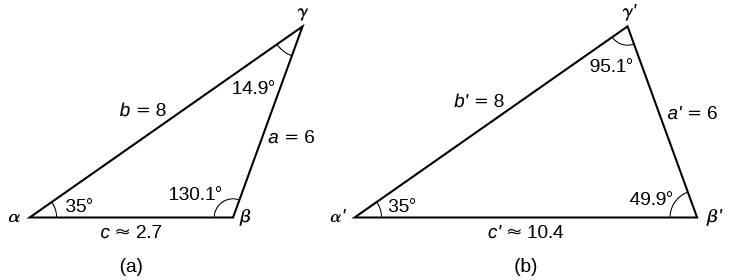
However, we were looking for the values for the triangle with an obtuse angle We can see them in the first triangle (a) in [link] .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?