0.1 Proofs, identities, and toolkit functions

<< Chapter < Page

Algebra and trigonometry Page 1 / 1

Chapter >> Page >

Appendix

Important proofs and derivations

Product Rule

$\log_{a} x y = \log_{a} x + \log_{a} y$

Proof:

Let $m = \log_{a} x$ and $n = \log_{a} y .$

Write in exponent form.

$x = a^{m}$ and $y = a^{n} .$

Multiply.

$x y = a^{m} a^{n} = a^{m + n}$

$\begin{matrix} a^{m + n} & = & x y \\ \log_{a} (x y) & = & m + n \\ = & \log_{a} x + \log_{b} y \end{matrix}$

Change of Base Rule

$\begin{array}{l} \log_{a} b = \frac{\log_{c} b}{\log_{c} a} \\ \log_{a} b = \frac{1}{\log_{b} a} \end{array}$

where $x$ and $y$ are positive, and $a > 0, a \neq 1.$

Proof:

Let $x = \log_{a} b .$

Write in exponent form.

$a^{x} = b$

Take the $\log_{c}$ of both sides.

$\begin{matrix} \log_{c} a^{x} & = & \log_{c} b \\ x \log_{c} a & = & \log_{c} b \\ x & = & \frac{\log_{c} b}{\log_{c} a} \\ \log_{a} b & = & \frac{\log_{c} b}{\log_{a} b} \end{matrix}$

When $c = b,$

$\log_{a} b = \frac{\log_{b} b}{\log_{b} a} = \frac{1}{\log_{b} a}$

Heron’s Formula

$A = \sqrt{s (s - a) (s - b) (s - c)}$

where $s = \frac{a + b + c}{2}$

Proof:

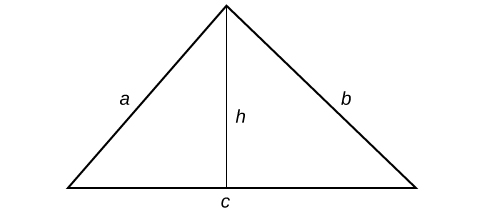
Let $a,$ $b,$ and $c$ be the sides of a triangle, and $h$ be the height.

A triangle with sides labeled: a, b and c. A line runs through the center of the triangle, bisecting the top angle; this line is labeled: h.

So $s = \frac{a + b + c}{2}$ .

We can further name the parts of the base in each triangle established by the height such that $p + q = c .$

A triangle with sides labeled: a, b, and c. A line runs through the center of the triangle bisecting the angle at the top; this line is labeled: h. The two new line segments on the base of the triangle are labeled: p and q.

Using the Pythagorean Theorem, $h^{2} + p^{2} = a^{2}$ and $h^{2} + q^{2} = b^{2} .$

Since $q = c - p,$ then $q^{2} = {(c - p)}^{2} .$ Expanding, we find that $q^{2} = c^{2} - 2 c p + p^{2} .$

We can then add $h^{2}$ to each side of the equation to get $h^{2} + q^{2} = h^{2} + c^{2} - 2 c p + p^{2} .$

Substitute this result into the equation $h^{2} + q^{2} = b^{2}$ yields $b^{2} = h^{2} + c^{2} - 2 c p + p^{2} .$

Then replacing $h^{2} + p^{2}$ with $a^{2}$ gives $b^{2} = a^{2} - 2 c p + c^{2} .$

Solve for $p$ to get

$p = \frac{a^{2} + b^{2} - c^{2}}{2 c}$

Since $h^{2} = a^{2} - p^{2},$ we get an expression in terms of $a,$ $b,$ and $c .$

$\begin{matrix} h^{2} & = & a^{2} - p^{2} \\ = & (a + p) (a - p) \\ = & [a + \frac{(a^{2} + c^{2} - b^{2})}{2 c}] [a - \frac{(a^{2} + c^{2} - b^{2})}{2 c}] \\ = & \frac{(2 a c + a^{2} + c^{2} - b^{2}) (2 a c - a^{2} - c^{2} + b^{2})}{4 c^{2}} \\ = & \frac{({(a + c)}^{2} - b^{2}) (b^{2} - {(a - c)}^{2})}{4 c^{2}} \\ = & \frac{(a + b + c) (a + c - b) (b + a - c) (b - a + c)}{4 c^{2}} \\ = & \frac{(a + b + c) (- a + b + c) (a - b + c) (a + b - c)}{4 c^{2}} \\ = & \frac{2 s \cdot (2 s - a) \cdot (2 s - b) (2 s - c)}{4 c^{2}} \end{matrix}$

Therefore,

$\begin{matrix} h^{2} & = & \frac{4 s (s - a) (s - b) (s - c)}{c^{2}} \\ h & = & \frac{2 \sqrt{s (s - a) (s - b) (s - c)}}{c} \end{matrix}$

And since $A = \frac{1}{2} c h,$ then

$\begin{matrix} A & = & \frac{1}{2} c \frac{2 \sqrt{s (s - a) (s - b) (s - c)}}{c} \\ = & \sqrt{s (s - a) (s - b) (s - c)} \end{matrix}$

Properties of the Dot Product

$u \cdot v = v \cdot u$

Proof:

$\begin{matrix} u \cdot v & = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ v_{1}, v_{2}, ... v_{n} ⟩ \\ = u_{1} v_{1} + u_{2} v_{2} + ... + u_{n} v_{n} \\ = v_{1} u_{1} + v_{2} u_{2} + ... + v_{n} v_{n} \\ = ⟨ v_{1}, v_{2}, ... v_{n} ⟩ \cdot ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \\ = v \cdot u \end{matrix}$

$u \cdot (v + w) = u \cdot v + u \cdot w$

Proof:

$\begin{matrix} u \cdot (v + w) & = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot (⟨ v_{1}, v_{2}, ... v_{n} ⟩ + ⟨ w_{1}, w_{2}, ... w_{n} ⟩) \\ = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ v_{1} + w_{1}, v_{2} + w_{2}, ... v_{n} + w_{n} ⟩ \\ = ⟨ u_{1} (v_{1} + w_{1}), u_{2} (v_{2} + w_{2}), ... u_{n} (v_{n} + w_{n}) ⟩ \\ = ⟨ u_{1} v_{1} + u_{1} w_{1}, u_{2} v_{2} + u_{2} w_{2}, ... u_{n} v_{n} + u_{n} w_{n} ⟩ \\ = ⟨ u_{1} v_{1}, u_{2} v_{2}, ..., u_{n} v_{n} ⟩ + ⟨ u_{1} w_{1}, u_{2} w_{2}, ..., u_{n} w_{n} ⟩ \\ = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ v_{1}, v_{2}, ... v_{n} ⟩ + ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ w_{1}, w_{2}, ... w_{n} ⟩ \\ = u \cdot v + u \cdot w \end{matrix}$

$u \cdot u = {| u |}^{2}$

Proof:

$\begin{matrix} u \cdot u & = ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \cdot ⟨ u_{1}, u_{2}, ... u_{n} ⟩ \\ = u_{1} u_{1} + u_{2} u_{2} + ... + u_{n} u_{n} \\ = u_{1}^{2} + u_{2}^{2} + ... + u_{n}^{2} \\ = | ⟨ u_{1}, u_{2}, ... u_{n} ⟩ |^{2} \\ = v \cdot u \end{matrix}$

Standard Form of the Ellipse centered at the Origin

$1 = \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$

Derivation

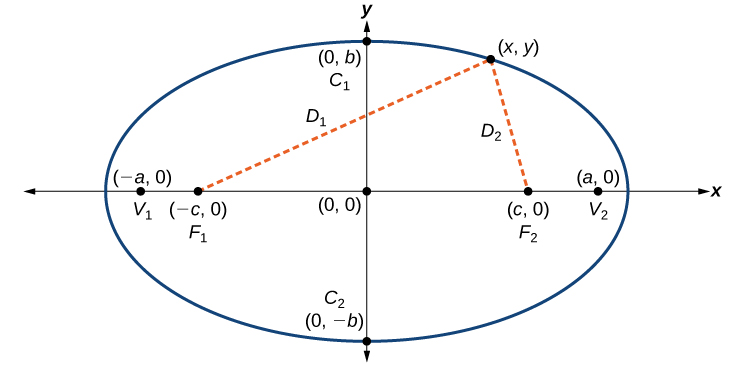
An ellipse consists of all the points for which the sum of distances from two foci is constant:

$\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = constant$

An ellipse centered at the origin on an x, y-coordinate plane. Points C1 and C2 are plotted at the points (0, b) and (0, -b) respectively; these points appear on the ellipse. Points V1 and V2 are plotted at the points (-a, 0) and (a, 0) respectively; these points appear on the ellipse. Points F1 and F2 are plotted at the points (-c, 0) and (c, 0) respectively; these points appear on the x-axis, but not the ellipse. The point (x, y) appears on the ellipse in the first quadrant. Dotted lines extend from F1 and F2 to the point (x, y).

Consider a vertex.

An ellipse centered at the origin. The points C1 and C2 are plotted at the points (0, b) and (0, -b) respectively; these points are on the ellipse. The points V1 and V2 are plotted at the points (-a, 0) and (a, 0) respectively; these points are on the ellipse. The points F1 and F2 are plotted at the points (-c, 0) and (c, 0) respectively; these points are on the x-axis and not on the ellipse. A line extends from the point F1 to a point (x, y) which is at the point (a, 0). A line extends from the point F2 to the point (x, y) as well.

Then, $\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = 2 a$

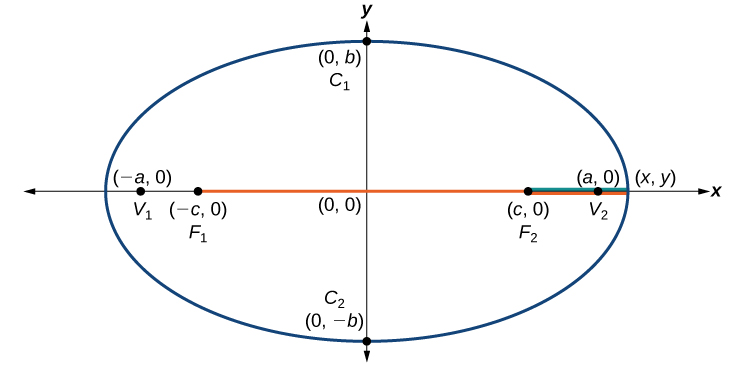
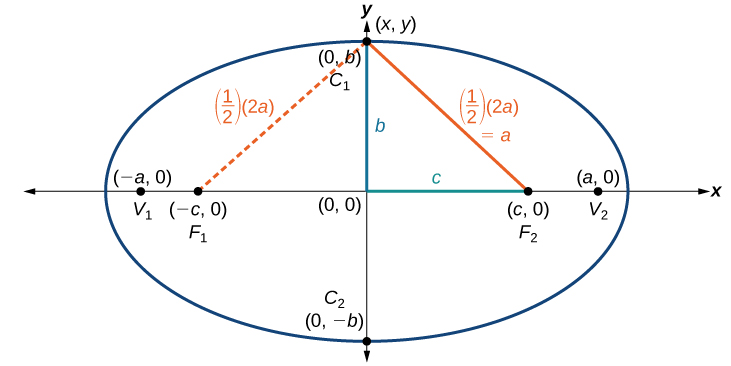
Consider a covertex.

Then $b^{2} + c^{2} = a^{2} .$

$\begin{matrix} \sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} & = & 2 a - \sqrt{{(x - c)}^{2} + y^{2}} \\ {(x + c)}^{2} + y^{2} & = & {(2 a - \sqrt{{(x - c)}^{2} + y^{2}})}^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} + {(x - c)}^{2} + y^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} + x^{2} - 2 c x + y^{2} \\ 2 c x & = & 4 a^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} - 2 c x \\ 4 c x - 4 a^{2} & = & 4 a \sqrt{{(x - c)}^{2} + y^{2}} \\ - \frac{1}{4 a} (4 c x - 4 a^{2}) & = & \sqrt{{(x - c)}^{2} + y^{2}} \\ a - \frac{c}{a} x & = & \sqrt{{(x - c)}^{2} + y^{2}} \\ a^{2} - 2 x c + \frac{c^{2}}{a^{2}} x^{2} & = & {(x - c)}^{2} + y^{2} \\ a^{2} - 2 x c + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} - 2 x c + c^{2} + y^{2} \\ a^{2} + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} + c^{2} + y^{2} \\ a^{2} + \frac{c^{2}}{a^{2}} x^{2} & = & x^{2} + c^{2} + y^{2} \\ a^{2} - c^{2} & = & x^{2} - \frac{c^{2}}{a^{2}} x^{2} + y^{2} \\ a^{2} - c^{2} & = & x^{2} (1 - \frac{c^{2}}{a^{2}}) + y^{2} \end{matrix}$

Let $1 = \frac{a^{2}}{a^{2}} .$

\begin{matrix} a^{2} - c^{2} & = & x^{2} (\frac{a^{2} - c^{2}}{a^{2}}) + y^{2} \\ 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - c^{2}} \end{matrix}

Because $b^{2} + c^{2} = a^{2},$ then $b^{2} = a^{2} - c^{2} .$

\begin{matrix} 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - c^{2}} \\ 1 & = & \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} \end{matrix}

Standard Form of the Hyperbola

$1 = \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$

Derivation

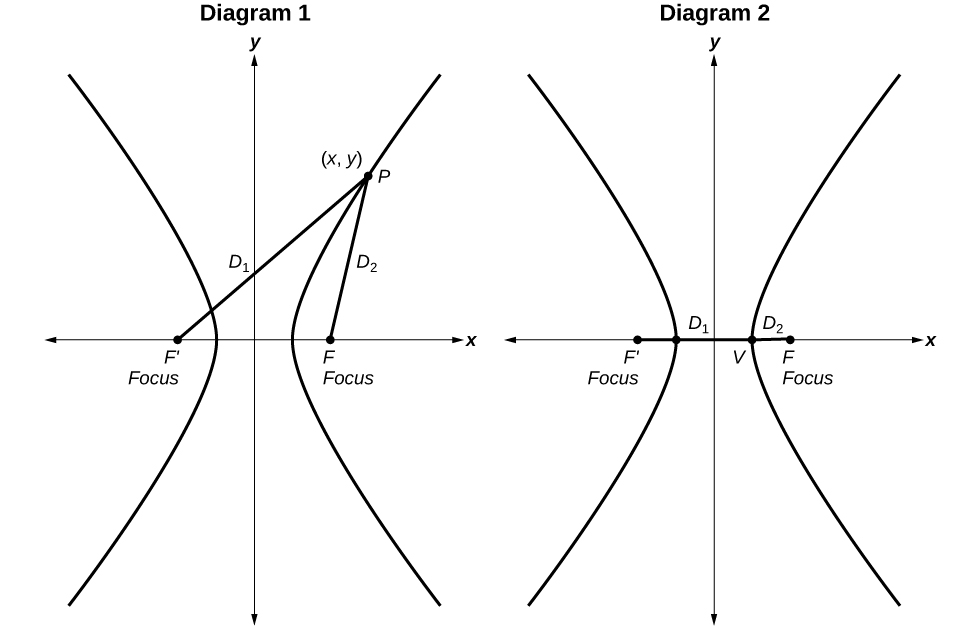
A hyperbola is the set of all points in a plane such that the absolute value of the difference of the distances between two fixed points is constant.

Side-by-side graphs of hyperbole. In Diagram 1: The foci F’ and F are labeled and can be found a little in front of the opening of the hyperbola. A point P at (x,y) on the right curve is labeled. A line extends from the F’ focus to the point P labeled: D1. A line extends from the F focus to the point P labeled: D2. In Diagram 2: The foci F’ and F are labeled and can be found a little in front of the opening of the hyperbola. A point V is labeled at the vertex of the right hyperbola. A line extends from the F’ focus to the point V labeled: D1. A line extends from the F focus to the point V labeled: D2.

Diagram 1: The difference of the distances from Point P to the foci is constant:

$\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = constant$

Diagram 2: When the point is a vertex, the difference is $2 a .$

$\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = 2 a$

$\begin{matrix} \sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} - \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} - \sqrt{{(x - c)}^{2} + y^{2}} & = & 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} & = & 2 a + \sqrt{{(x - c)}^{2} + y^{2}} \\ {(x + c)}^{2} + y^{2} & = & (2 a + \sqrt{{(x - c)}^{2} + y^{2}}) \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2}} + y^{2} \\ x^{2} + 2 c x + c^{2} + y^{2} & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2} + y^{2}} + x^{2} - 2 c x + y^{2} \\ 2 c x & = & 4 a^{2} + 4 a \sqrt{{(x - c)}^{2} + y^{2}} - 2 c x \\ 4 c x - 4 a^{2} & = & 4 a \sqrt{{(x - c)}^{2} + y^{2}} \\ c x - a^{2} & = & a \sqrt{{(x - c)}^{2} + y^{2}} \\ {(c x - a^{2})}^{2} & = & a^{2} ({(x - c)}^{2} + y^{2}) \\ c^{2} x^{2} - 2 a^{2} c^{2} x^{2} + a^{4} & = & a^{2} x^{2} - 2 a^{2} c^{2} x^{2} + a^{2} c^{2} + a^{2} y^{2} \\ c^{2} x^{2} + a^{4} & = & a^{2} x^{2} + a^{2} c^{2} + a^{2} y^{2} \\ a^{4} - a^{2} c^{2} & = & a^{2} x^{2} - c^{2} x^{2} + a^{2} y^{2} \\ a^{2} (a^{2} - c^{2}) & = & (a^{2} - c^{2}) x^{2} + a^{2} y^{2} \\ a^{2} (a^{2} - c^{2}) & = & (c^{2} - a^{2}) x^{2} - a^{2} y^{2} \end{matrix}$

Define $b$ as a positive number such that $b^{2} = c^{2} - a^{2} .$

\begin{matrix} a^{2} b^{2} & = & b^{2} x^{2} - a^{2} y^{2} \\ \frac{a^{2} b^{2}}{a^{2} b^{2}} & = & \frac{b^{2} x^{2}}{a^{2} b^{2}} - \frac{a^{2} y^{2}}{a^{2} b^{2}} \\ 1 & = & \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} \end{matrix}

Trigonometric identities

Pythagorean Identity	$\begin{array}{l} \cos^{2} t + \sin^{2} t = 1 \\ 1 + \tan^{2} t = \sec^{2} t \\ 1 + \cot^{2} t = \csc^{2} t \end{array}$
Even-Odd Identities	$\begin{array}{l} \cos (- t) = c o s t \\ \sec (- t) = \sec t \\ \sin (- t) = - \sin t \\ \tan (- t) = - \tan t \\ \csc (- t) = - \csc t \\ \cot (- t) = - \cot t \end{array}$
Cofunction Identities	$\begin{array}{l} \cos t = \sin (\frac{π}{2} - t) \\ \sin t = \cos (\frac{π}{2} - t) \\ \tan t = \cot (\frac{π}{2} - t) \\ \cot t = \tan (\frac{π}{2} - t) \\ \sec t = \csc (\frac{π}{2} - t) \\ \csc t = \sec (\frac{π}{2} - t) \end{array}$
Fundamental Identities	$\begin{array}{l} \tan t = \frac{\sin t}{\cos t} \\ \sec t = \frac{1}{\cos t} \\ \csc t = \frac{1}{\sin t} \\ c o t t = \frac{1}{tan t} = \frac{cos t}{sin t} \end{array}$
Sum and Difference Identities	$\begin{array}{l} \cos (α + β) = \cos α \cos β - \sin α \sin β \\ \cos (α - β) = \cos α \cos β + \sin α \sin β \\ \sin (α + β) = \sin α \cos β + \cos α \sin β \\ \sin (α - β) = \sin α \cos β - \cos α \sin β \\ \tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \tan β} \\ \tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \tan β} \end{array}$
Double-Angle Formulas	$\begin{array}{l} \sin (2 θ) = 2 \sin θ \cos θ \\ \cos (2 θ) = \cos^{2} θ - \sin^{2} θ \\ \cos (2 θ) = 1 - 2 \sin^{2} θ \\ \cos (2 θ) = 2 \cos^{2} θ - 1 \\ \tan (2 θ) = \frac{2 \tan θ}{1 - \tan^{2} θ} \end{array}$
Half-Angle Formulas	$\begin{array}{l} \sin \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{2}} \\ \cos \frac{α}{2} = \pm \sqrt{\frac{1 + \cos α}{2}} \\ \tan \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{1 + \cos α}} \\ \tan \frac{α}{2} = \frac{\sin α}{1 + \cos α} \\ \tan \frac{α}{2} = \frac{1 - \cos α}{\sin α} \end{array}$
Reduction Formulas	$\begin{array}{l} \sin^{2} θ = \frac{1 - \cos (2 θ)}{2} \\ \cos^{2} θ = \frac{1 + \cos (2 θ)}{2} \\ \tan^{2} θ = \frac{1 - \cos (2 θ)}{1 + \cos (2 θ)} \end{array}$
Product-to-Sum Formulas	$\begin{array}{l} \cos α \cos β = \frac{1}{2} [\cos (α - β) + \cos (α + β)] \\ \sin α \cos β = \frac{1}{2} [\sin (α + β) + \sin (α - β)] \\ \sin α \sin β = \frac{1}{2} [\cos (α - β) - \cos (α + β)] \\ \cos α \sin β = \frac{1}{2} [\sin (α + β) - \sin (α - β)] \end{array}$
Sum-to-Product Formulas	$\begin{array}{l} \sin α + \sin β = 2 \sin (\frac{α + β}{2}) \cos (\frac{α - β}{2}) \\ \sin α - \sin β = 2 \sin (\frac{α - β}{2}) \cos (\frac{α + β}{2}) \\ \cos α - \cos β = - 2 \sin (\frac{α + β}{2}) \sin (\frac{α - β}{2}) \\ \cos α + \cos β = 2 \cos (\frac{α + β}{2}) \cos (\frac{α - β}{2}) \end{array}$
Law of Sines	$\begin{array}{l} \frac{\sin α}{a} = \frac{\sin β}{b} = \frac{\sin γ}{c} \\ \frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ} \end{array}$
Law of Cosines	$\begin{matrix} a^{2} = b^{2} + c^{2} - 2 b c \cos α \\ b^{2} = a^{2} + c^{2} - 2 a c \cos β \\ c^{2} = a^{2} + b^{2} - 2 a b cos γ \end{matrix}$

Toolkit functions

Three graphs side-by-side. From left to right, graph of the identify function, square function, and square root function. All three graphs extend from -4 to 4 on each axis.

Three graphs side-by-side. From left to right, graph of the cubic function, cube root function, and reciprocal function. All three graphs extend from -4 to 4 on each axis.

Three graphs side-by-side. From left to right, graph of the absolute value function, exponential function, and natural logarithm function. All three graphs extend from -4 to 4 on each axis.

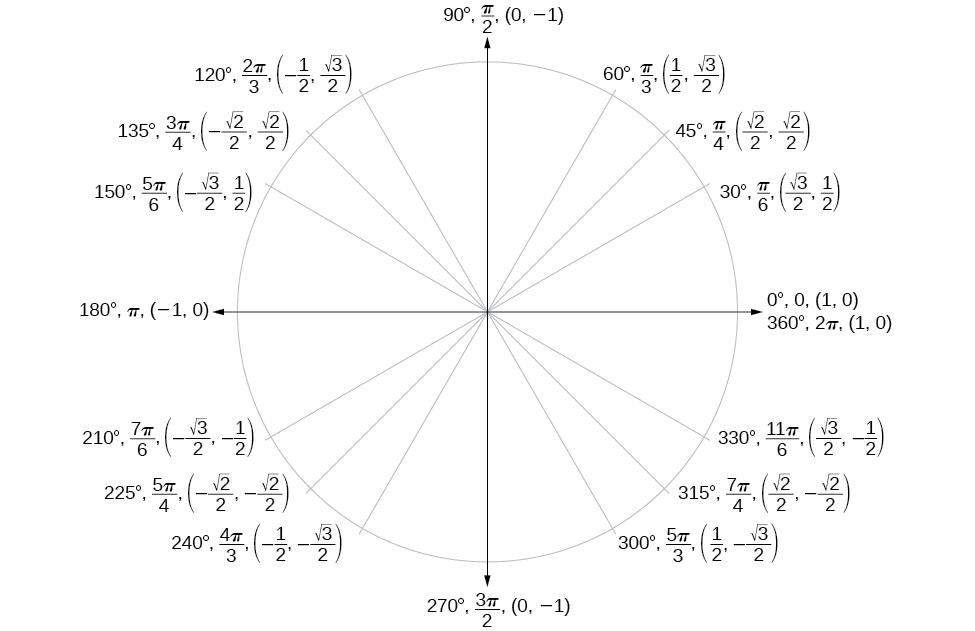
Trigonometric functions

Unit Circle

Angle	$0$	$\frac{π}{6}, or 30 °$	$\frac{π}{4}, or 45 °$	$\frac{π}{3}, or 60 °$	$\frac{π}{2}, or 90 °$
Cosine	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
Sine	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
Tangent	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$	Undefined
Secant	1	$\frac{2 \sqrt{3}}{3}$	$\sqrt{2}$	2	Undefined
Cosecant	Undefined	2	$\sqrt{2}$	$\frac{2 \sqrt{3}}{3}$	1
Cotangent	Undefined	$\sqrt{3}$	1	$\frac{\sqrt{3}}{3}$	0

Questions & Answers

Why is b in the answer

Dahsolar Reply

how do you work it out?

Brad Reply

answer

Ernest

heheheehe

Nitin

(Pcos∅+qsin∅)/(pcos∅-psin∅)

John Reply

how to do that?

Rosemary Reply

what is it about?

Amoah

how to answer the activity

Chabelita Reply

how to solve the activity

Chabelita

solve for X,,4^X-6(2^)-16=0

Alieu Reply

x4xminus 2

Lominate

sobhan Singh jina uniwarcity tignomatry ka long answers tile questions

harish Reply

t he silly nut company makes two mixtures of nuts: mixture a and mixture b. a pound of mixture a contains 12 oz of peanuts, 3 oz of almonds and 1 oz of cashews and sells for $4. a pound of mixture b contains 12 oz of peanuts, 2 oz of almonds and 2 oz of cashews and sells for $5. the company has 1080

ZAHRO Reply

If  , , are the roots of the equation 3 2 0, x px qx r     Find the value of 1  .

Swetha Reply

Parts of a pole were painted red, blue and yellow. 3/5 of the pole was red and 7/8 was painted blue. What part was painted yellow?

Patrick Reply

Parts of the pole was painted red, blue and yellow. 3 /5 of the pole was red and 7 /8 was painted blue. What part was painted yellow?

Patrick

how I can simplify algebraic expressions

Katleho Reply

Lairene and Mae are joking that their combined ages equal Sam’s age. If Lairene is twice Mae’s age and Sam is 69 yrs old, what are Lairene’s and Mae’s ages?

Mary Reply

23yrs

Yeboah

lairenea's age is 23yrs

ACKA

Katleho

Ello everyone

Katleho

Laurene is 46 yrs and Mae is 23 is

Solomon

hey people

christopher

age does not matter

christopher

solve for X, 4^x-6(2*)-16=0

Alieu

prove`x^3-3x-2cosA=0 (-π<A<=π

Mayank Reply

create a lesson plan about this lesson

Rose Reply

Excusme but what are you wrot?

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Algebra and trigonometry. OpenStax CNX. Nov 14, 2016 Download for free at https://legacy.cnx.org/content/col11758/1.6

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?

Ask

	SCJP Online Exam 310-065 By Prateek Ashtikar Start Quiz
	Elementary algebra By OpenStax Read Online Course
	NCE Ch 06 Groups By Anh Dao Start Quiz
	Computer Skills Literacy MCQ By LaToya Trowers Start Quiz
©flickr: anjelkam	Art By Caitlyn Gobble Start Exam
	1 Arts Society: Theater 1 By Jonathan Long Start Quiz
	Microbiology Practice Test By Sandhills MLT Start Test
©flickr: Abraham	2 Biology 2 By Sarah Warren Start Test
	9 Psychology MCQ 2011 2 Exam By John Gabrieli Start Exam
	Concepts of biology By OpenStax Read Online Course