| << Chapter < Page | Chapter >> Page > |
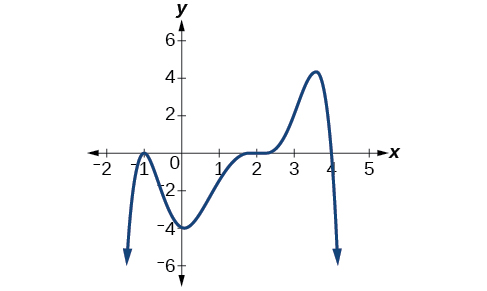
Given the graph shown in [link] , write a formula for the function shown.
With quadratics, we were able to algebraically find the maximum or minimum value of the function by finding the vertex. For general polynomials, finding these turning points is not possible without more advanced techniques from calculus. Even then, finding where extrema occur can still be algebraically challenging. For now, we will estimate the locations of turning points using technology to generate a graph.
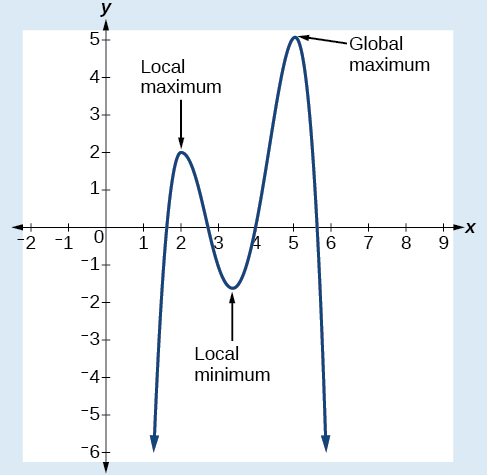
Each turning point represents a local minimum or maximum. Sometimes, a turning point is the highest or lowest point on the entire graph. In these cases, we say that the turning point is a global maximum or a global minimum . These are also referred to as the absolute maximum and absolute minimum values of the function.
A local maximum or local minimum at (sometimes called the relative maximum or minimum, respectively) is the output at the highest or lowest point on the graph in an open interval around If a function has a local maximum at then for all in an open interval around If a function has a local minimum at then for all in an open interval around
A global maximum or global minimum is the output at the highest or lowest point of the function. If a function has a global maximum at then for all If a function has a global minimum at then for all
We can see the difference between local and global extrema in [link] .
Do all polynomial functions have a global minimum or maximum?
No. Only polynomial functions of even degree have a global minimum or maximum. For example, has neither a global maximum nor a global minimum.
An open-top box is to be constructed by cutting out squares from each corner of a 14 cm by 20 cm sheet of plastic then folding up the sides. Find the size of squares that should be cut out to maximize the volume enclosed by the box.
We will start this problem by drawing a picture like that in [link] , labeling the width of the cut-out squares with a variable,
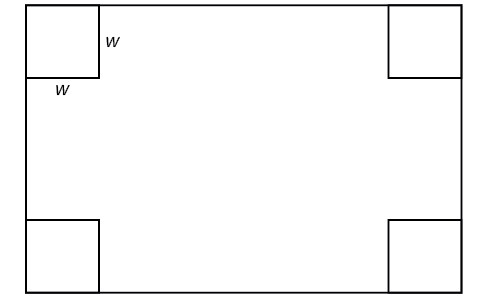
Notice that after a square is cut out from each end, it leaves a cm by cm rectangle for the base of the box, and the box will be cm tall. This gives the volume
Notice, since the factors are and the three zeros are 10, 7, and 0, respectively. Because a height of 0 cm is not reasonable, we consider the only the zeros 10 and 7. The shortest side is 14 and we are cutting off two squares, so values may take on are greater than zero or less than 7. This means we will restrict the domain of this function to Using technology to sketch the graph of on this reasonable domain, we get a graph like that in [link] . We can use this graph to estimate the maximum value for the volume, restricted to values for that are reasonable for this problem—values from 0 to 7.
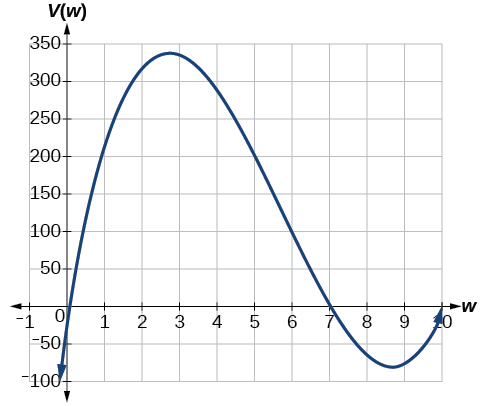
From this graph, we turn our focus to only the portion on the reasonable domain, We can estimate the maximum value to be around 340 cubic cm, which occurs when the squares are about 2.75 cm on each side. To improve this estimate, we could use advanced features of our technology, if available, or simply change our window to zoom in on our graph to produce [link] .
![Graph of V(w)=(20-2w)(14-2w)w where the x-axis is labeled w and the y-axis is labeled V(w) on the domain [2.4, 3].](/ocw/mirror/col11667/m49347/CNX_Precalc_Figure_03_04_029.jpg)
From this zoomed-in view, we can refine our estimate for the maximum volume to about 339 cubic cm, when the squares measure approximately 2.7 cm on each side.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?