| << Chapter < Page | Chapter >> Page > |
A child randomly selects 3 gumballs from a container holding 4 purple gumballs, 8 yellow gumballs, and 2 green gumballs.
Access these online resources for additional instruction and practice with probability.
Visit this website for additional practice questions from Learningpod.
| probability of an event with equally likely outcomes | |
| probability of the union of two events | |
| probability of the union of mutually exclusive events | |
| probability of the complement of an event |
What term is used to express the likelihood of an event occurring? Are there restrictions on its values? If so, what are they? If not, explain.
probability; The probability of an event is restricted to values between and inclusive of and
What is a sample space?
What is an experiment?
An experiment is an activity with an observable result.
What is the difference between events and outcomes? Give an example of both using the sample space of tossing a coin 50 times.
The union of two sets is defined as a set of elements that are present in at least one of the sets. How is this similar to the definition used for the union of two events from a probability model? How is it different?
The probability of the union of two events occurring is a number that describes the likelihood that at least one of the events from a probability model occurs. In both a union of sets and a union of events the union includes either or both. The difference is that a union of sets results in another set, while the union of events is a probability, so it is always a numerical value between and
For the following exercises, use the spinner shown in [link] to find the probabilities indicated.
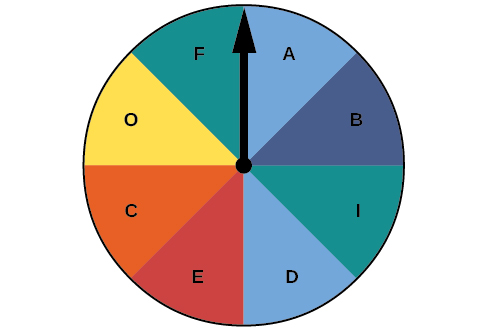
Landing on red

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?