| << Chapter < Page | Chapter >> Page > |
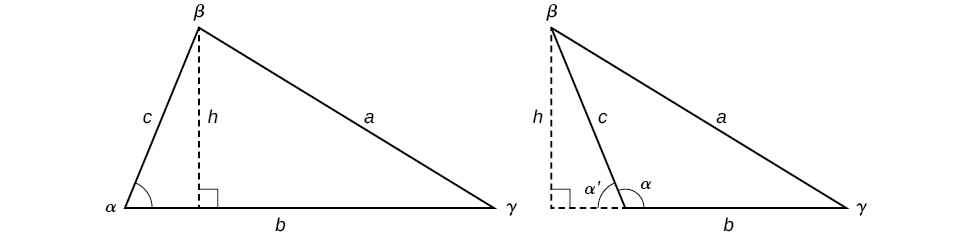
Thus,
Similarly,
The formula for the area of an oblique triangle is given by
This is equivalent to one-half of the product of two sides and the sine of their included angle.
Find the area of a triangle with sides and angle Round the area to the nearest integer.
Using the formula, we have
Find the area of the triangle given Round the area to the nearest tenth.
about
The more we study trigonometric applications, the more we discover that the applications are countless. Some are flat, diagram-type situations, but many applications in calculus, engineering, and physics involve three dimensions and motion.
Find the altitude of the aircraft in the problem introduced at the beginning of this section, shown in [link] . Round the altitude to the nearest tenth of a mile.
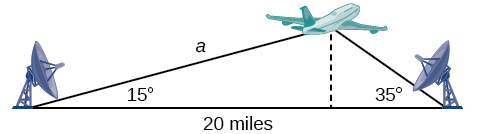
To find the elevation of the aircraft, we first find the distance from one station to the aircraft, such as the side and then use right triangle relationships to find the height of the aircraft,
Because the angles in the triangle add up to 180 degrees, the unknown angle must be 180°−15°−35°=130°. This angle is opposite the side of length 20, allowing us to set up a Law of Sines relationship.
The distance from one station to the aircraft is about 14.98 miles.
Now that we know we can use right triangle relationships to solve for
The aircraft is at an altitude of approximately 3.9 miles.
The diagram shown in [link] represents the height of a blimp flying over a football stadium. Find the height of the blimp if the angle of elevation at the southern end zone, point A, is 70°, the angle of elevation from the northern end zone, point is 62°, and the distance between the viewing points of the two end zones is 145 yards.
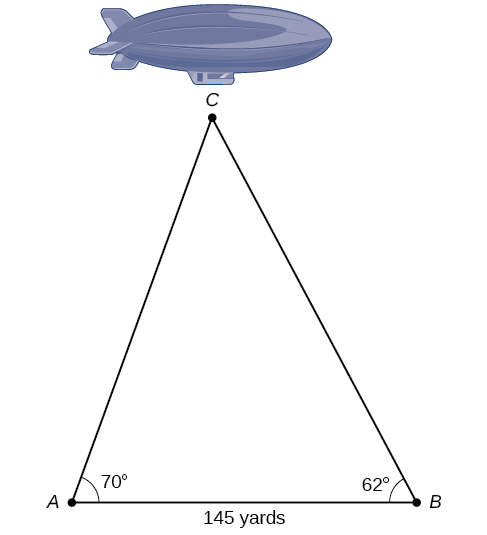
161.9 yd.
Access these online resources for additional instruction and practice with trigonometric applications.
| Law of Sines | |
| Area for oblique triangles |

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?