| << Chapter < Page | Chapter >> Page > |
To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of between a line of sight to the top of the tree and the ground, as shown in [link] . Find the height of the tree.

We know that the angle of elevation is and the adjacent side is 30 ft long. The opposite side is the unknown height.
The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of letting be the unknown height.
The tree is approximately 46 feet tall.
How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of with the ground? Round to the nearest foot.
About 52 ft
Access these online resources for additional instruction and practice with right triangle trigonometry.
Visit this website for additional practice questions from Learningpod.
| Cofunction Identities |
For the given right triangle, label the adjacent side, opposite side, and hypotenuse for the indicated angle.
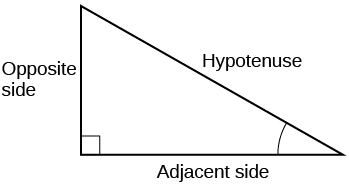
When a right triangle with a hypotenuse of 1 is placed in the unit circle, which sides of the triangle correspond to the x - and y -coordinates?
The tangent of an angle compares which sides of the right triangle?
The tangent of an angle is the ratio of the opposite side to the adjacent side.
What is the relationship between the two acute angles in a right triangle?
Explain the cofunction identity.
For example, the sine of an angle is equal to the cosine of its complement; the cosine of an angle is equal to the sine of its complement.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?