| << Chapter < Page | Chapter >> Page > |
Access the following online resource for additional instruction and practice with graphs of parametric equations.
What are two methods used to graph parametric equations?
plotting points with the orientation arrow and a graphing calculator
What is one difference in point-plotting parametric equations compared to Cartesian equations?
Why are some graphs drawn with arrows?
The arrows show the orientation, the direction of motion according to increasing values of
Name a few common types of graphs of parametric equations.
Why are parametric graphs important in understanding projectile motion?
The parametric equations show the different vertical and horizontal motions over time.
For the following exercises, graph each set of parametric equations by making a table of values. Include the orientation on the graph.
For the following exercises, sketch the curve and include the orientation.
For the following exercises, graph the equation and include the orientation. Then, write the Cartesian equation.
For the following exercises, graph the equation and include the orientation.
For the following exercises, use the parametric equations for integers a and b :
Graph on the domain where and and include the orientation.
Graph on the domain where and , and include the orientation.
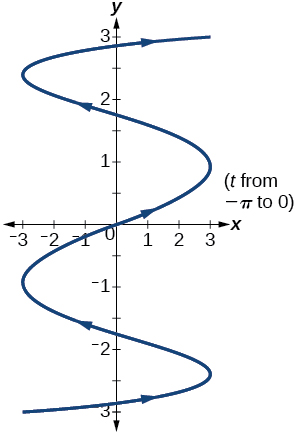
Graph on the domain where and , and include the orientation.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?