| << Chapter < Page | Chapter >> Page > |
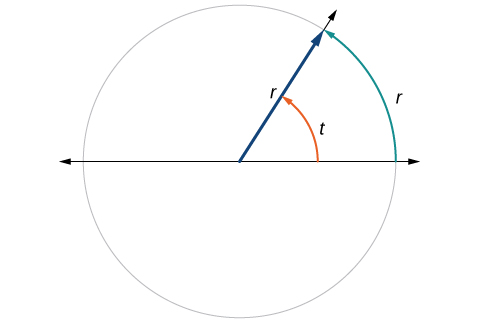
This brings us to our new angle measure. One radian is the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle. A central angle is an angle formed at the center of a circle by two radii. Because the total circumference equals times the radius, a full circular rotation is radians. So
See [link] . Note that when an angle is described without a specific unit, it refers to radian measure. For example, an angle measure of 3 indicates 3 radians. In fact, radian measure is dimensionless, since it is the quotient of a length (circumference) divided by a length (radius) and the length units cancel out.
An arc length is the length of the curve along the arc. Just as the full circumference of a circle always has a constant ratio to the radius, the arc length produced by any given angle also has a constant relation to the radius, regardless of the length of the radius.
This ratio, called the radian measure , is the same regardless of the radius of the circle—it depends only on the angle. This property allows us to define a measure of any angle as the ratio of the arc length to the radius See [link] .
If then
To elaborate on this idea, consider two circles, one with radius 2 and the other with radius 3. Recall the circumference of a circle is where is the radius. The smaller circle then has circumference and the larger has circumference Now we draw a 45° angle on the two circles, as in [link] .
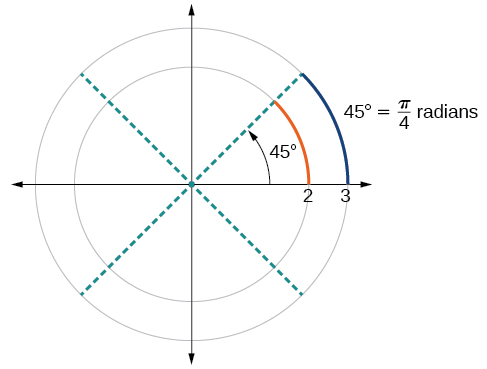
Notice what happens if we find the ratio of the arc length divided by the radius of the circle.
Since both ratios are the angle measures of both circles are the same, even though the arc length and radius differ.
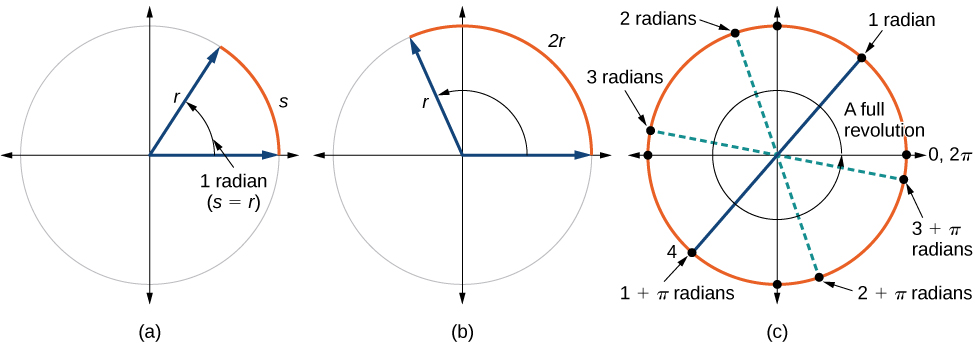
One radian is the measure of the central angle of a circle such that the length of the arc between the initial side and the terminal side is equal to the radius of the circle. A full revolution (360°) equals radians. A half revolution (180°) is equivalent to radians.
The radian measure of an angle is the ratio of the length of the arc subtended by the angle to the radius of the circle. In other words, if is the length of an arc of a circle, and is the radius of the circle, then the central angle containing that arc measures radians. In a circle of radius 1, the radian measure corresponds to the length of the arc.
A measure of 1 radian looks to be about 60°. Is that correct?
Yes. It is approximately 57.3°. Because radians equals 360°, radian equals

Notification Switch
Would you like to follow the 'Contemporary math applications' conversation and receive update notifications?