| << Chapter < Page | Chapter >> Page > |
| x | f(x) |
| 1 | 409.4 |
| 2 | 260.7 |
| 3 | 170.4 |
| 4 | 110.6 |
| 5 | 74 |
| 6 | 44.7 |
| 7 | 32.4 |
| 8 | 19.5 |
| 9 | 12.7 |
| 10 | 8.1 |
| x | f(x) |
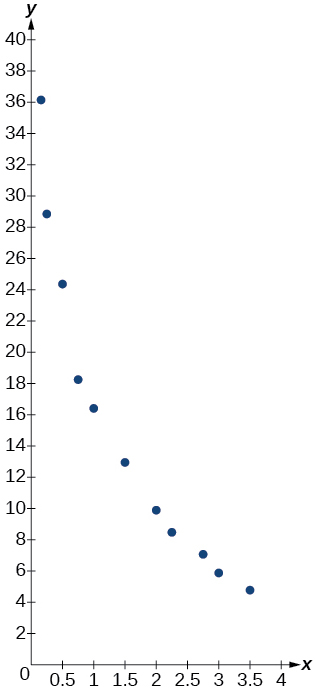
| 0.15 | 36.21 |
| 0.25 | 28.88 |
| 0.5 | 24.39 |
| 0.75 | 18.28 |
| 1 | 16.5 |
| 1.5 | 12.99 |
| 2 | 9.91 |
| 2.25 | 8.57 |
| 2.75 | 7.23 |
| 3 | 5.99 |
| 3.5 | 4.81 |
logarithmic;
| x | f(x) |
| 0 | 9 |
| 2 | 22.6 |
| 4 | 44.2 |
| 5 | 62.1 |
| 7 | 96.9 |
| 8 | 113.4 |
| 10 | 133.4 |
| 11 | 137.6 |
| 15 | 148.4 |
| 17 | 149.3 |
The population of a pod of bottlenose dolphins is modeled by the function where is given in years. To the nearest whole number, what will the pod population be after years?
About dolphins.
Find an exponential equation that passes through the points and
Drew wants to save $2,500 to go to the next World Cup. To the nearest dollar, how much will he need to invest in an account now with APR, compounding daily, in order to reach his goal in years?
An investment account was opened with an initial deposit of $9,600 and earns interest, compounded continuously. How much will the account be worth after years?
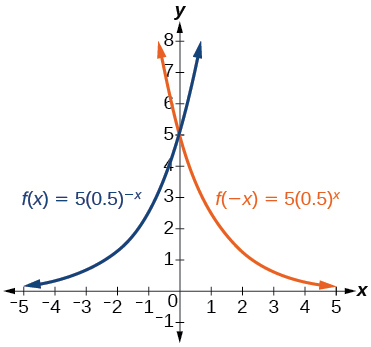
Graph the function and its reflection across the y -axis on the same axes, and give the y -intercept.
y -intercept:
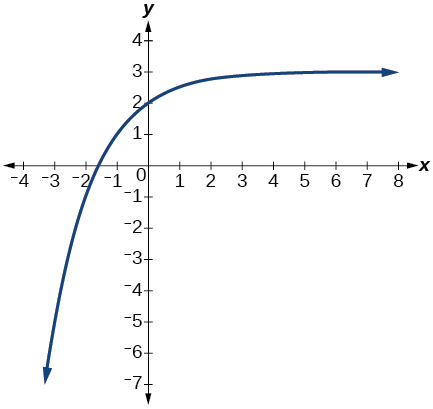
The graph shows transformations of the graph of What is the equation for the transformation?
Rewrite as an equivalent logarithmic equation.
Solve for by converting the logarithmic equation to exponential form.
Evaluate without using a calculator.
Evaluate using a calculator. Round to the nearest thousandth.
Graph the function
State the domain, vertical asymptote, and end behavior of the function
Domain: Vertical asymptote: End behavior: and
Rewrite as a sum.
Rewrite as a product.
Condense the expression to a single logarithm.
Rewrite as a logarithm. Then apply the change of base formula to solve for using the natural log. Round to the nearest thousandth.
Solve by rewriting each side with a common base.
Use logarithms to find the exact solution for . If there is no solution, write no solution .
Find the exact solution for If there is no solution, write no solution .
Find the exact solution for If there is no solution, write no solution .
no solution
Find the exact solution for If there is no solution, write no solution .
Find the exact solution for If there is no solution, write no solution .
Use the definition of a logarithm to find the exact solution for
Use the one-to-one property of logarithms to find an exact solution for If there is no solution, write no solution .
The formula for measuring sound intensity in decibels is defined by the equation where is the intensity of the sound in watts per square meter and is the lowest level of sound that the average person can hear. How many decibels are emitted from a rock concert with a sound intensity of watts per square meter?
A radiation safety officer is working with grams of a radioactive substance. After days, the sample has decayed to grams. Rounding to five significant digits, write an exponential equation representing this situation. To the nearest day, what is the half-life of this substance?
half-life: about days
Write the formula found in the previous exercise as an equivalent equation with base Express the exponent to five significant digits.
A bottle of soda with a temperature of Fahrenheit was taken off a shelf and placed in a refrigerator with an internal temperature of After ten minutes, the internal temperature of the soda was Use Newton’s Law of Cooling to write a formula that models this situation. To the nearest degree, what will the temperature of the soda be after one hour?
The population of a wildlife habitat is modeled by the equation where is given in years. How many animals were originally transported to the habitat? How many years will it take before the habitat reaches half its capacity?
Enter the data from [link] into a graphing calculator and graph the resulting scatter plot. Determine whether the data from the table would likely represent a function that is linear, exponential, or logarithmic.
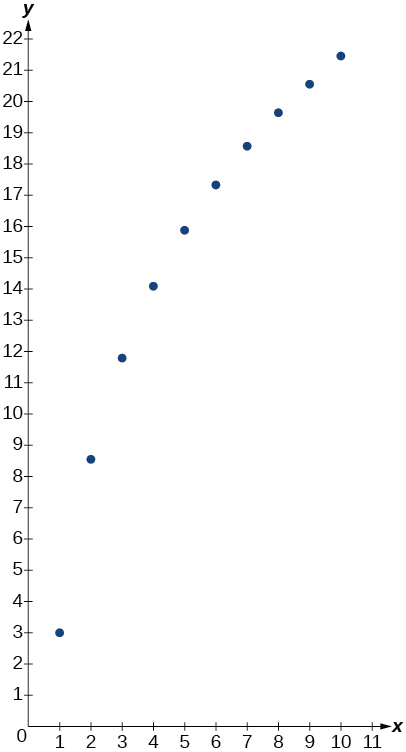
| x | f(x) |
| 1 | 3 |
| 2 | 8.55 |
| 3 | 11.79 |
| 4 | 14.09 |
| 5 | 15.88 |
| 6 | 17.33 |
| 7 | 18.57 |
| 8 | 19.64 |
| 9 | 20.58 |
| 10 | 21.42 |
logarithmic
The population of a lake of fish is modeled by the logistic equation where is time in years. To the nearest hundredth, how many years will it take the lake to reach of its carrying capacity?
For the following exercises, use a graphing utility to create a scatter diagram of the data given in the table. Observe the shape of the scatter diagram to determine whether the data is best described by an exponential, logarithmic, or logistic model. Then use the appropriate regression feature to find an equation that models the data. When necessary, round values to five decimal places.
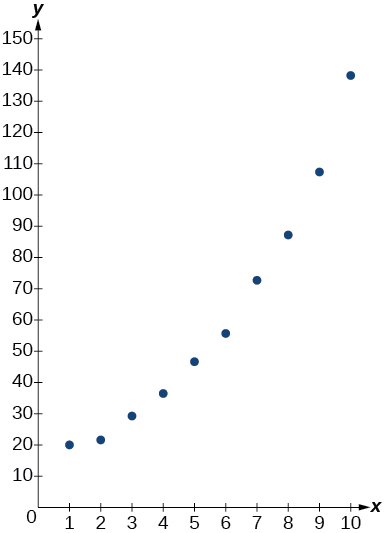
| x | f(x) |
| 1 | 20 |
| 2 | 21.6 |
| 3 | 29.2 |
| 4 | 36.4 |
| 5 | 46.6 |
| 6 | 55.7 |
| 7 | 72.6 |
| 8 | 87.1 |
| 9 | 107.2 |
| 10 | 138.1 |
exponential;
| x | f(x) |
| 3 | 13.98 |
| 4 | 17.84 |
| 5 | 20.01 |
| 6 | 22.7 |
| 7 | 24.1 |
| 8 | 26.15 |
| 9 | 27.37 |
| 10 | 28.38 |
| 11 | 29.97 |
| 12 | 31.07 |
| 13 | 31.43 |
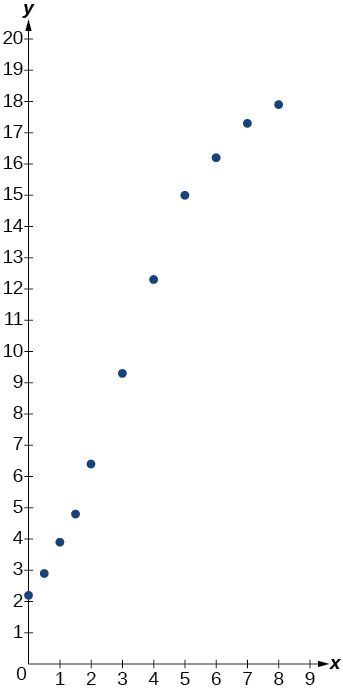
| x | f(x) |
| 0 | 2.2 |
| 0.5 | 2.9 |
| 1 | 3.9 |
| 1.5 | 4.8 |
| 2 | 6.4 |
| 3 | 9.3 |
| 4 | 12.3 |
| 5 | 15 |
| 6 | 16.2 |
| 7 | 17.3 |
| 8 | 17.9 |
logistic;

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?