| << Chapter < Page | Chapter >> Page > |
“God made the integers; all else is the work of man.” This rather famous quote by nineteenth-century German mathematician Leopold Kronecker sets the stage for this section on the polar form of a complex number. Complex numbers were invented by people and represent over a thousand years of continuous investigation and struggle by mathematicians such as Pythagoras , Descartes , De Moivre, Euler , Gauss , and others. Complex numbers answered questions that for centuries had puzzled the greatest minds in science.
We first encountered complex numbers in Complex Numbers . In this section, we will focus on the mechanics of working with complex numbers: translation of complex numbers from polar form to rectangular form and vice versa, interpretation of complex numbers in the scheme of applications, and application of De Moivre’s Theorem.
Plotting a complex number is similar to plotting a real number, except that the horizontal axis represents the real part of the number, and the vertical axis represents the imaginary part of the number,
Given a complex number plot it in the complex plane.
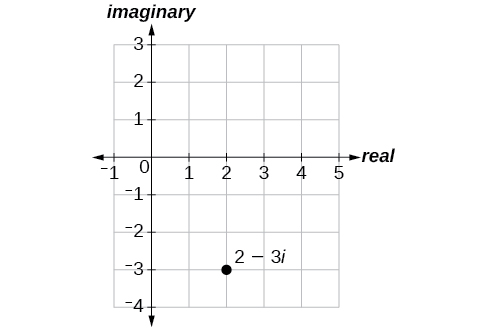
Plot the complex number in the complex plane .
From the origin, move two units in the positive horizontal direction and three units in the negative vertical direction. See [link] .
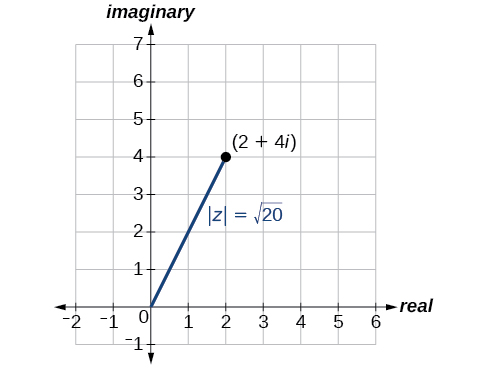
The first step toward working with a complex number in polar form is to find the absolute value. The absolute value of a complex number is the same as its magnitude , or It measures the distance from the origin to a point in the plane. For example, the graph of in [link] , shows
Given a complex number, the absolute value of is defined as
It is the distance from the origin to the point
Notice that the absolute value of a real number gives the distance of the number from 0, while the absolute value of a complex number gives the distance of the number from the origin,
Find the absolute value of
Given find

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?