| << Chapter < Page | Chapter >> Page > |
For the following exercises, explain the notation in words. The volume of a tank of gasoline, in gallons, minutes after noon.
At 12:30 p.m. , the rate of change of the number of gallons in the tank is –20 gallons per minute. That is, the tank is losing 20 gallons per minute.
At 200 minutes after noon, the volume of gallons in the tank is changing at the rate of 30 gallons per minute.
For the following exercises, explain the functions in words. The height, of a projectile after seconds is given by
The height of the projectile is zero at and again at In other words, the projectile starts on the ground and falls to earth again after 5 seconds.
For the following exercises, the volume of a sphere with respect to its radius is given by
Find the average rate of change of as changes from 1 cm to 2 cm.
For the following exercises, the revenue generated by selling items is given by
Find the average change of the revenue function as changes from to
Find and interpret.
$50.00 per unit, which is the instantaneous rate of change of revenue when exactly 10 units are sold.
Find and interpret. Compare to and explain the difference.
For the following exercises, the cost of producing cellphones is described by the function
Find the average rate of change in the total cost as changes from
$21 per unit
Find the approximate marginal cost, when 15 cellphones have been produced, of producing the 16 th cellphone.
Find the approximate marginal cost, when 20 cellphones have been produced, of producing the 21 st cellphone.
$36
For the following exercises, use the definition for the derivative at a point to find the derivative of the functions.
For the following exercises, use [link] .
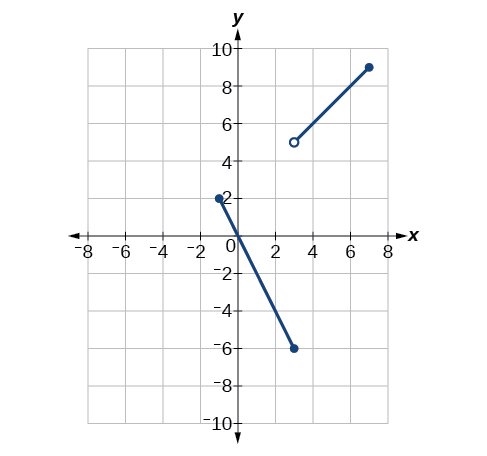
At what values of is the function discontinuous? What condition of continuity is violated?
Using [link] , estimate
| −0.1 | 2.875 |
| −0.01 | 2.92 |
| −0.001 | 2.998 |
| 0 | Undefined |
| 0.001 | 2.9987 |
| 0.01 | 2.865 |
| 0.1 | 2.78145 |
| 0.15 | 2.678 |
3
For the following exercises, with the use of a graphing utility, use numerical or graphical evidence to determine the left- and right-hand limits of the function given as approaches If the function has limit as approaches state it. If not, discuss why there is no limit.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?