| << Chapter < Page | Chapter >> Page > |
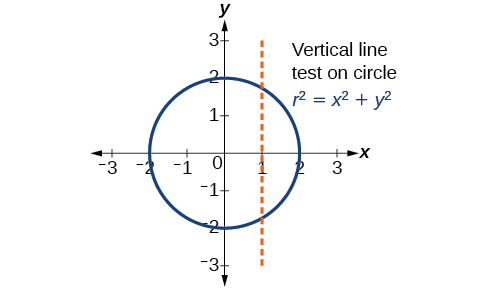
However, if we were to graph each equation on its own, each one would pass the vertical line test and therefore would represent a function. In some instances, the concept of breaking up the equation for a circle into two functions is similar to the concept of creating parametric equations, as we use two functions to produce a non-function. This will become clearer as we move forward.
Suppose is a number on an interval, The set of ordered pairs, where and forms a plane curve based on the parameter The equations and are the parametric equations.
Parameterize the curve letting Graph both equations.
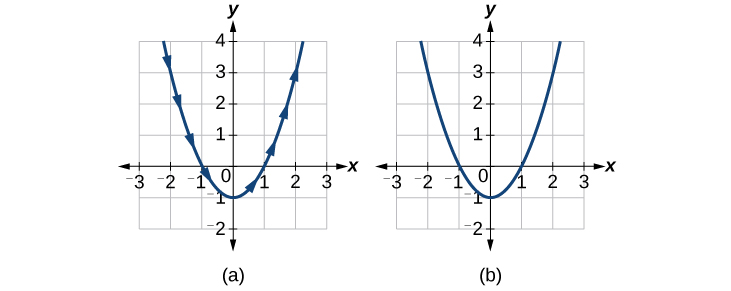
If then to find we replace the variable with the expression given in In other words, Make a table of values similar to [link] , and sketch the graph.
See the graphs in [link] . It may be helpful to use the TRACE feature of a graphing calculator to see how the points are generated as increases.
Construct a table of values and plot the parametric equations:
Find a pair of parametric equations that models the graph of using the parameter Plot some points and sketch the graph.
If and we substitute for into the equation, then Our pair of parametric equations is
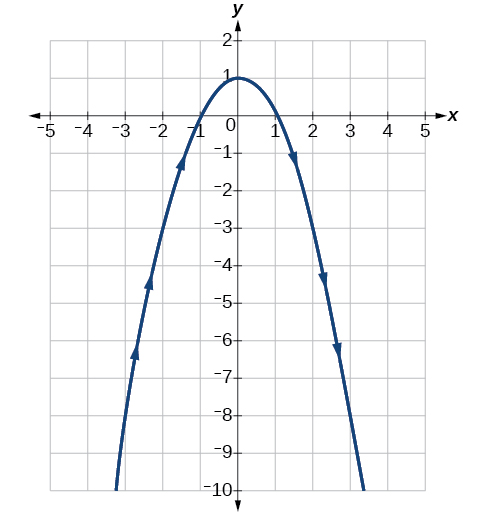
To graph the equations, first we construct a table of values like that in [link] . We can choose values around from to The values in the column will be the same as those in the column because Calculate values for the column
The graph of is a parabola facing downward, as shown in [link] . We have mapped the curve over the interval shown as a solid line with arrows indicating the orientation of the curve according to Orientation refers to the path traced along the curve in terms of increasing values of As this parabola is symmetric with respect to the line the values of are reflected across the y -axis.
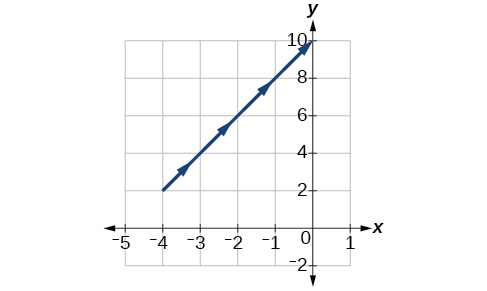
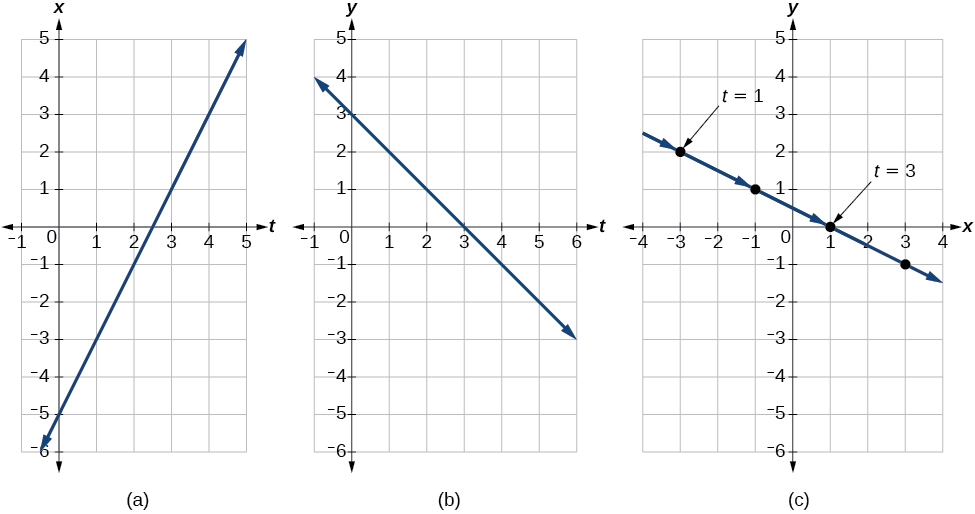
An object travels at a steady rate along a straight path to in the same plane in four seconds. The coordinates are measured in meters. Find parametric equations for the position of the object.
The parametric equations are simple linear expressions, but we need to view this problem in a step-by-step fashion. The x -value of the object starts at meters and goes to 3 meters. This means the distance x has changed by 8 meters in 4 seconds, which is a rate of or We can write the x -coordinate as a linear function with respect to time as In the linear function template and
Similarly, the y -value of the object starts at 3 and goes to which is a change in the distance y of −4 meters in 4 seconds, which is a rate of or We can also write the y -coordinate as the linear function Together, these are the parametric equations for the position of the object, where and are expressed in meters and represents time:
Using these equations, we can build a table of values for and (see [link] ). In this example, we limited values of to non-negative numbers. In general, any value of can be used.
From this table, we can create three graphs, as shown in [link] .

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?