1. Home
  2. Precalculus
  3. Trigonometric identities and
  4. Sum and difference identities

7.2 Sum and difference identities

<< Chapter < Page
  Precalculus     Page 1 / 6
Chapter >> Page >
In this section, you will:
  • Use sum and difference formulas for cosine.
  • Use sum and difference formulas for sine.
  • Use sum and difference formulas for tangent.
  • Use sum and difference formulas for cofunctions.
  • Use sum and difference formulas to verify identities.
Photo of Mt. McKinley.
Mount McKinley, in Denali National Park, Alaska, rises 20,237 feet (6,168 m) above sea level. It is the highest peak in North America. (credit: Daniel A. Leifheit, Flickr)

How can the height of a mountain be measured? What about the distance from Earth to the sun? Like many seemingly impossible problems, we rely on mathematical formulas to find the answers. The trigonometric identities, commonly used in mathematical proofs, have had real-world applications for centuries, including their use in calculating long distances.

The trigonometric identities we will examine in this section can be traced to a Persian astronomer who lived around 950 AD, but the ancient Greeks discovered these same formulas much earlier and stated them in terms of chords. These are special equations or postulates, true for all values input to the equations, and with innumerable applications.

In this section, we will learn techniques that will enable us to solve problems such as the ones presented above. The formulas that follow will simplify many trigonometric expressions and equations. Keep in mind that, throughout this section, the term formula is used synonymously with the word identity .

Using the sum and difference formulas for cosine

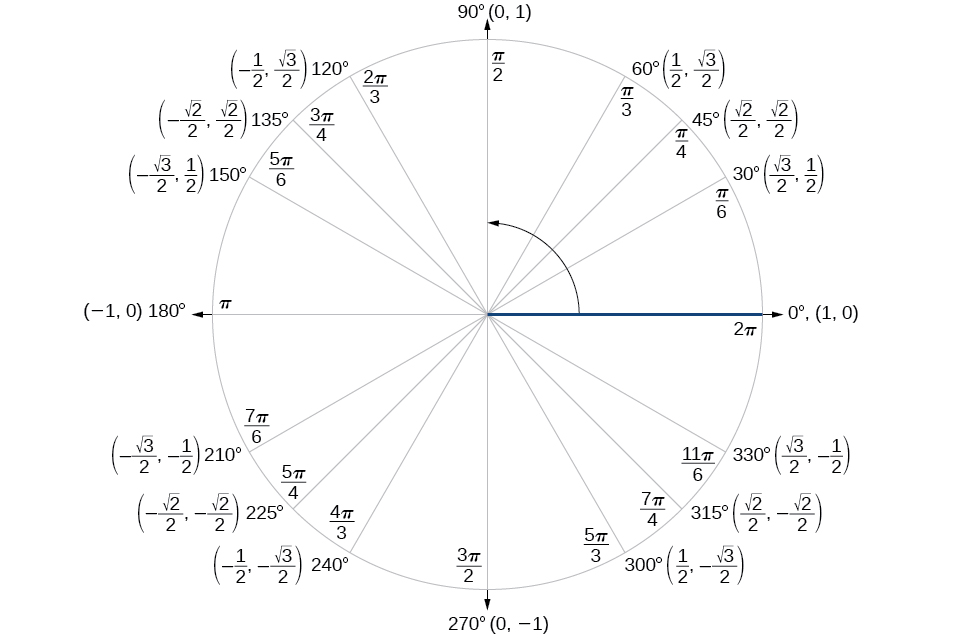
Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite the given angle in terms of two angles that have known trigonometric values. We can use the special angles , which we can review in the unit circle shown in [link] .

Diagram of the unit circle with points labeled on its edge. P point is at an angle a from the positive x axis with coordinates (cosa, sina). Point Q is at an angle of B from the positive x axis with coordinates (cosb, sinb). Angle POQ is a - B degrees. Point A is at an angle of (a-B) from the x axis with coordinates (cos(a-B), sin(a-B)). Point B is just at point (1,0). Angle AOB is also a - B degrees. Radii PO, AO, QO, and BO are all 1 unit long and are the legs of triangles POQ and AOB. Triangle POQ is a rotation of triangle AOB, so the distance from P to Q is the same as the distance from A to B.
The Unit Circle

We will begin with the sum and difference formulas for cosine , so that we can find the cosine of a given angle if we can break it up into the sum or difference of two of the special angles. See [link] .

Sum formula for cosine cos ( α + β ) = cos   α   cos   β − sin   α   sin   β
Difference formula for cosine cos ( α − β ) = cos   α   cos   β + sin   α   sin   β

First, we will prove the difference formula for cosines. Let’s consider two points on the unit circle. See [link] . Point   P   is at an angle   α   from the positive x- axis with coordinates   ( cos   α , sin   α )   and point   Q   is at an angle of   β   from the positive x- axis with coordinates   ( cos   β , sin   β ) .   Note the measure of angle   P O Q   is   α − β .  

Label two more points:   A   at an angle of   ( α − β )   from the positive x- axis with coordinates   ( cos ( α − β ) , sin ( α − β ) ) ;   and point   B   with coordinates   ( 1 , 0 ) .   Triangle   P O Q   is a rotation of triangle   A O B   and thus the distance from   P   to   Q   is the same as the distance from   A   to   B .

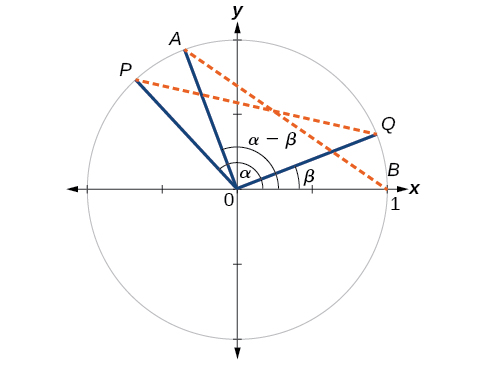
Diagram of the unit circle with points labeled on its edge. P point is at an angle a from the positive x axis with coordinates (cosa, sina). Point Q is at an angle of B from the positive x axis with coordinates (cosb, sinb). Angle POQ is a - B degrees. Point A is at an angle of (a-B) from the x axis with coordinates (cos(a-B), sin(a-B)). Point B is just at point (1,0). Angle AOB is also a - B degrees. Radii PO, AO, QO, and BO are all 1 unit long and are the legs of triangles POQ and AOB. Triangle POQ is a rotation of triangle AOB, so the distance from P to Q is the same as the distance from A to B.

We can find the distance from   P   to   Q   using the distance formula .

d P Q = ( cos   α − cos   β ) 2 + ( sin   α − sin   β ) 2         = cos 2 α − 2   cos   α   cos   β + cos 2 β + sin 2 α − 2   sin   α   sin   β + sin 2 β

Then we apply the Pythagorean identity and simplify.

= ( cos 2 α + sin 2 α ) + ( cos 2 β + sin 2 β ) − 2   cos   α   cos   β − 2   sin   α   sin   β = 1 + 1 − 2   cos   α   cos   β − 2   sin   α   sin   β = 2 − 2   cos   α   cos   β − 2   sin   α   sin   β

Similarly, using the distance formula we can find the distance from   A   to   B .

Questions & Answers

for the "hiking" mix, there are 1,000 pieces in the mix, containing 390.8 g of fat, and 165 g of protein. if there is the same amount of almonds as cashews, how many of each item is in the trail mix?
ADNAN Reply
linear speed of an object
Melissa Reply
an object is traveling around a circle with a radius of 13 meters .if in 20 seconds a central angle of 1/7 Radian is swept out what are the linear and angular speed of the object
Melissa
test
Matrix
how to find domain
Mohamed Reply
like this: (2)/(2-x) the aim is to see what will not be compatible with this rational expression. If x= 0 then the fraction is undefined since we cannot divide by zero. Therefore, the domain consist of all real numbers except 2.
Dan
define the term of domain
Moha
if a>0 then the graph is concave
Angel Reply
if a<0 then the graph is concave blank
Angel
what's a domain
Kamogelo Reply
The set of all values you can use as input into a function su h that the output each time will be defined, meaningful and real.
Spiro
how fast can i understand functions without much difficulty
Joe Reply
what is inequalities
Nathaniel
functions can be understood without a lot of difficulty. Observe the following: f(2) 2x - x 2(2)-2= 2 now observe this: (2,f(2)) ( 2, -2) 2(-x)+2 = -2 -4+2=-2
Dan
what is set?
Kelvin Reply
a colony of bacteria is growing exponentially doubling in size every 100 minutes. how much minutes will it take for the colony of bacteria to triple in size
Divya Reply
I got 300 minutes. is it right?
Patience
no. should be about 150 minutes.
Jason
It should be 158.5 minutes.
Mr
ok, thanks
Patience
100•3=300 300=50•2^x 6=2^x x=log_2(6) =2.5849625 so, 300=50•2^2.5849625 and, so, the # of bacteria will double every (100•2.5849625) = 258.49625 minutes
Thomas
158.5 This number can be developed by using algebra and logarithms. Begin by moving log(2) to the right hand side of the equation like this: t/100 log(2)= log(3) step 1: divide each side by log(2) t/100=1.58496250072 step 2: multiply each side by 100 to isolate t. t=158.49
Dan
what is the importance knowing the graph of circular functions?
Arabella Reply
can get some help basic precalculus
ismail Reply
What do you need help with?
Andrew
how to convert general to standard form with not perfect trinomial
Camalia Reply
can get some help inverse function
ismail
Rectangle coordinate
Asma Reply
how to find for x
Jhon Reply
it depends on the equation
Robert
yeah, it does. why do we attempt to gain all of them one side or the other?
Melissa
how to find x: 12x = 144 notice how 12 is being multiplied by x. Therefore division is needed to isolate x and whatever we do to one side of the equation we must do to the other. That develops this: x= 144/12 divide 144 by 12 to get x. addition: 12+x= 14 subtract 12 by each side. x =2
Dan
whats a domain
mike Reply
The domain of a function is the set of all input on which the function is defined. For example all real numbers are the Domain of any Polynomial function.
Spiro
Spiro; thanks for putting it out there like that, 😁
Melissa
foci (–7,–17) and (–7,17), the absolute value of the differenceof the distances of any point from the foci is 24.
Churlene Reply
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Precalculus. OpenStax CNX. Jan 19, 2016 Download for free at https://legacy.cnx.org/content/col11667/1.6
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Precalculus' conversation and receive update notifications?

Ask