| << Chapter < Page | Chapter >> Page > |
When does an extraneous solution occur? How can an extraneous solution be recognized?
When can the one-to-one property of logarithms be used to solve an equation? When can it not be used?
The one-to-one property can be used if both sides of the equation can be rewritten as a single logarithm with the same base. If so, the arguments can be set equal to each other, and the resulting equation can be solved algebraically. The one-to-one property cannot be used when each side of the equation cannot be rewritten as a single logarithm with the same base.
For the following exercises, use like bases to solve the exponential equation.
For the following exercises, use logarithms to solve.
For the following exercises, use the definition of a logarithm to rewrite the equation as an exponential equation.
For the following exercises, use the definition of a logarithm to solve the equation.
For the following exercises, use the one-to-one property of logarithms to solve.
For the following exercises, solve each equation for
For the following exercises, solve the equation for if there is a solution . Then graph both sides of the equation, and observe the point of intersection (if it exists) to verify the solution.
For the following exercises, solve for the indicated value, and graph the situation showing the solution point.
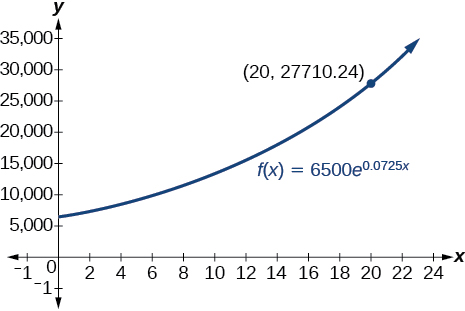
An account with an initial deposit of earns annual interest, compounded continuously. How much will the account be worth after 20 years?
about
The formula for measuring sound intensity in decibels is defined by the equation where is the intensity of the sound in watts per square meter and is the lowest level of sound that the average person can hear. How many decibels are emitted from a jet plane with a sound intensity of watts per square meter?
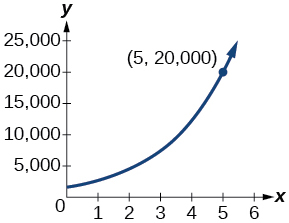
The population of a small town is modeled by the equation where is measured in years. In approximately how many years will the town’s population reach
about 5 years
For the following exercises, solve each equation by rewriting the exponential expression using the indicated logarithm. Then use a calculator to approximate to 3 decimal places .
using the common log.
using the common log
using the natural log
For the following exercises, use a calculator to solve the equation. Unless indicated otherwise, round all answers to the nearest ten-thousandth.
Atmospheric pressure in pounds per square inch is represented by the formula where is the number of miles above sea level. To the nearest foot, how high is the peak of a mountain with an atmospheric pressure of pounds per square inch? ( Hint : there are 5280 feet in a mile)
The magnitude M of an earthquake is represented by the equation where is the amount of energy released by the earthquake in joules and is the assigned minimal measure released by an earthquake. To the nearest hundredth, what would the magnitude be of an earthquake releasing joules of energy?
about
Use the definition of a logarithm along with the one-to-one property of logarithms to prove that
Recall the formula for continually compounding interest, Use the definition of a logarithm along with properties of logarithms to solve the formula for time such that is equal to a single logarithm.
Recall the compound interest formula Use the definition of a logarithm along with properties of logarithms to solve the formula for time
Newton’s Law of Cooling states that the temperature of an object at any time t can be described by the equation where is the temperature of the surrounding environment, is the initial temperature of the object, and is the cooling rate. Use the definition of a logarithm along with properties of logarithms to solve the formula for time such that is equal to a single logarithm.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?