| << Chapter < Page | Chapter >> Page > |
Given the value of a function at different points, calculate the average rate of change of a function for the interval between two values and
Using the data in [link] , find the average rate of change of the price of gasoline between 2007 and 2009.
In 2007, the price of gasoline was $2.84. In 2009, the cost was $2.41. The average rate of change is
Using the data in [link] , find the average rate of change between 2005 and 2010.
per year.
Given the function shown in [link] , find the average rate of change on the interval
At [link] shows At the graph shows
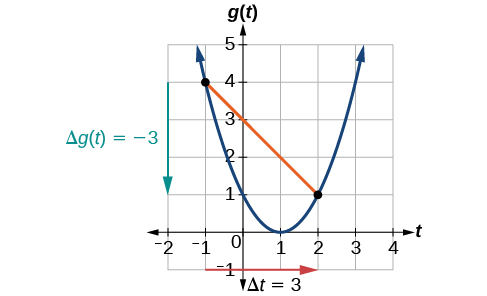
The horizontal change is shown by the red arrow, and the vertical change is shown by the turquoise arrow. The output changes by –3 while the input changes by 3, giving an average rate of change of
After picking up a friend who lives 10 miles away, Anna records her distance from home over time. The values are shown in [link] . Find her average speed over the first 6 hours.
| t (hours) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| D ( t ) (miles) | 10 | 55 | 90 | 153 | 214 | 240 | 282 | 300 |
Here, the average speed is the average rate of change. She traveled 282 miles in 6 hours, for an average speed of
The average speed is 47 miles per hour.
Compute the average rate of change of on the interval
We can start by computing the function values at each endpoint of the interval.
Now we compute the average rate of change.
The electrostatic force measured in newtons, between two charged particles can be related to the distance between the particles in centimeters, by the formula Find the average rate of change of force if the distance between the particles is increased from 2 cm to 6 cm.
We are computing the average rate of change of on the interval
The average rate of change is newton per centimeter.
Find the average rate of change of on the interval The answer will be an expression involving
We use the average rate of change formula.
This result tells us the average rate of change in terms of between and any other point For example, on the interval the average rate of change would be

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?