| << Chapter < Page | Chapter >> Page > |
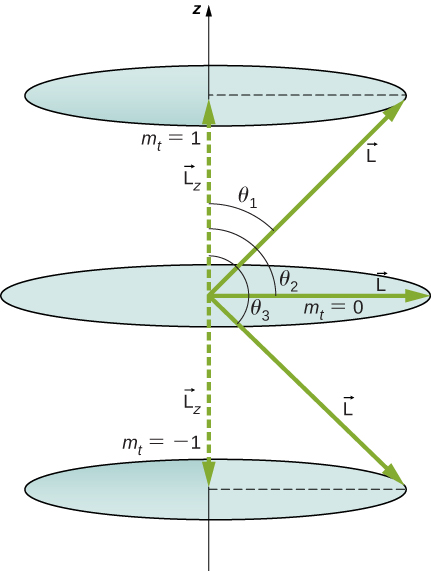
The quantity can have three values, given by .
As you can see in [link] , so for , we have
Thus,
Similarly, for , we find this gives
Then for :
so that
which approaches 1 as l becomes very large. If , then . Furthermore, for large l , there are many values of , so that all angles become possible as l gets very large.
Check Your Understanding Can the magnitude of ever be equal to L ?
No. The quantum number Thus, the magnitude of is always less than L because
As we saw earlier, we can use quantum mechanics to make predictions about physical events by the use of probability statements. It is therefore proper to state, “An electron is located within this volume with this probability at this time,” but not, “An electron is located at the position ( x , y , z ) at this time.” To determine the probability of finding an electron in a hydrogen atom in a particular region of space, it is necessary to integrate the probability density over that region:
where dV is an infinitesimal volume element. If this integral is computed for all space, the result is 1, because the probability of the particle to be located somewhere is 100% (the normalization condition). In a more advanced course on modern physics, you will find that where is the complex conjugate. This eliminates the occurrences of in the above calculation.
Consider an electron in a state of zero angular momentum ( ). In this case, the electron’s wave function depends only on the radial coordinate r . (Refer to the states and in [link] .) The infinitesimal volume element corresponds to a spherical shell of radius r and infinitesimal thickness dr , written as

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?