| << Chapter < Page | Chapter >> Page > |
Although a spherical mirror is shown in part (b) of [link] , comatic aberration occurs also for parabolic mirrors—it does not result from a breakdown in the small-angle approximation. Spherical aberration, however, occurs only for spherical mirrors and is a result of a breakdown in the small-angle approximation. We will discuss both coma and spherical aberration later in this chapter, in connection with telescopes.
At what distance is an image always located: at or f ?
Under what circumstances will an image be located at the focal point of a spherical lens or mirror?
when the object is at infinity; see the mirror equation
What is meant by a negative magnification? What is meant by a magnification whose absolute value is less than one?
Can an image be larger than the object even though its magnification is negative? Explain.
Yes, negative magnification simply means that the image is upside down; this does not prevent the image from being larger than the object. For instance, for a concave mirror, if distance to the object is larger than one focal distance but smaller than two focal distances the image will be inverted and magnified.
The following figure shows a light bulb between two spherical mirrors. One mirror produces a beam of light with parallel rays; the other keeps light from escaping without being put into the beam. Where is the filament of the light in relation to the focal point or radius of curvature of each mirror?

It is in the focal point of the big mirror and at the center of curvature of the small mirror.
Why are diverging mirrors often used for rearview mirrors in vehicles? What is the main disadvantage of using such a mirror compared with a flat one?
Some telephoto cameras use a mirror rather than a lens. What radius of curvature mirror is needed to replace a 800 mm-focal length telephoto lens?
Calculate the focal length of a mirror formed by the shiny back of a spoon that has a 3.00 cm radius of curvature.
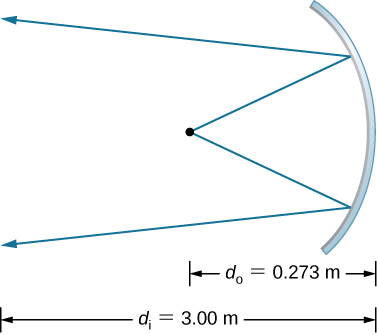
Electric room heaters use a concave mirror to reflect infrared (IR) radiation from hot coils. Note that IR radiation follows the same law of reflection as visible light. Given that the mirror has a radius of curvature of 50.0 cm and produces an image of the coils 3.00 m away from the mirror, where are the coils?
Find the magnification of the heater element in the previous problem. Note that its large magnitude helps spread out the reflected energy.
What is the focal length of a makeup mirror that produces a magnification of 1.50 when a person’s face is 12.0 cm away? Explicitly show how you follow the steps in the [link] .
Step 1: Image formation by a mirror is involved.
Step 2: Draw the problem set up when possible.
Step 3: Use thin-lens equations to solve this problem.
Step 4: Find f.
Step 5: Given:
.
Step 6: No ray tracing is needed.
Step 7: Using
. Then,
.
Step 8: The image is virtual because the image distance is negative. The focal length is positive, so the mirror is concave.
A shopper standing 3.00 m from a convex security mirror sees his image with a magnification of 0.250. (a) Where is his image? (b) What is the focal length of the mirror? (c) What is its radius of curvature?
An object 1.50 cm high is held 3.00 cm from a person’s cornea, and its reflected image is measured to be 0.167 cm high. (a) What is the magnification? (b) Where is the image? (c) Find the radius of curvature of the convex mirror formed by the cornea. (Note that this technique is used by optometrists to measure the curvature of the cornea for contact lens fitting. The instrument used is called a keratometer, or curve measurer.)
a. for a convex mirror
; b.
(behind the cornea);
c.
Ray tracing for a flat mirror shows that the image is located a distance behind the mirror equal to the distance of the object from the mirror. This is stated as , since this is a negative image distance (it is a virtual image). What is the focal length of a flat mirror?
Show that, for a flat mirror, , given that the image is the same distance behind the mirror as the distance of the object from the mirror.
Use the law of reflection to prove that the focal length of a mirror is half its radius of curvature. That is, prove that . Note this is true for a spherical mirror only if its diameter is small compared with its radius of curvature.
Referring to the electric room heater considered in problem 5, calculate the intensity of IR radiation in projected by the concave mirror on a person 3.00 m away. Assume that the heating element radiates 1500 W and has an area of , and that half of the radiated power is reflected and focused by the mirror.
Two mirrors are inclined at an angle of 60 and an object is placed at a point that is equidistant from the two mirrors. Use a protractor to draw rays accurately and locate all images. You may have to draw several figures so that that rays for different images do not clutter your drawing.
Two parallel mirrors are facing each other and are separated by a distance of 3 cm. A point object is placed between the mirrors 1 cm from one of the mirrors. Find the coordinates of all the images.

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?