| << Chapter < Page | Chapter >> Page > |
Third, the probability density distributions for a quantum oscillator in the ground low-energy state, , is largest at the middle of the well . For the particle to be found with greatest probability at the center of the well, we expect that the particle spends the most time there as it oscillates. This is opposite to the behavior of a classical oscillator, in which the particle spends most of its time moving with relative small speeds near the turning points.
Check Your Understanding Find the expectation value of the position for a particle in the ground state of a harmonic oscillator using symmetry.
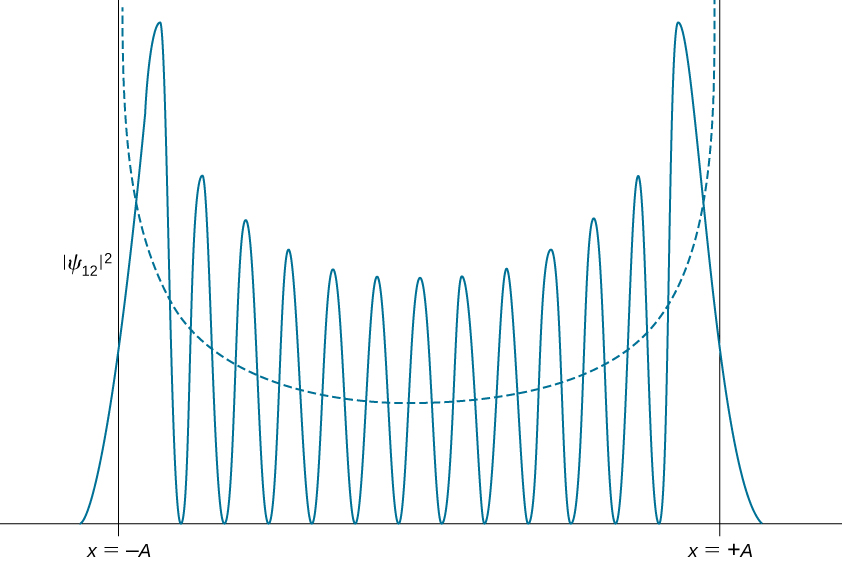
Quantum probability density distributions change in character for excited states, becoming more like the classical distribution when the quantum number gets higher. We observe this change already for the first excited state of a quantum oscillator because the distribution peaks up around the turning points and vanishes at the equilibrium position, as seen in [link] . In accordance with Bohr’s correspondence principle, in the limit of high quantum numbers, the quantum description of a harmonic oscillator converges to the classical description, which is illustrated in [link] . The classical probability density distribution corresponding to the quantum energy of the state is a reasonably good approximation of the quantum probability distribution for a quantum oscillator in this excited state. This agreement becomes increasingly better for highly excited states.
Is it possible to measure energy of for a quantum harmonic oscillator? Why? Why not? Explain.
No. This energy corresponds to , but n must be an integer.
Explain the connection between Planck’s hypothesis of energy quanta and the energies of the quantum harmonic oscillator.
If a classical harmonic oscillator can be at rest, why can the quantum harmonic oscillator never be at rest? Does this violate Bohr’s correspondence principle?
Because the smallest allowed value of the quantum number n for a simple harmonic oscillator is 0. No, because quantum mechanics and classical mechanics agree only in the limit of large .
Use an example of a quantum particle in a box or a quantum oscillator to explain the physical meaning of Bohr’s correspondence principle.
Can we simultaneously measure position and energy of a quantum oscillator? Why? Why not?
Yes, within the constraints of the uncertainty principle. If the oscillating particle is localized, the momentum and therefore energy of the oscillator are distributed.
Show that the two lowest energy states of the simple harmonic oscillator, and from [link] , satisfy [link] .
proof
If the ground state energy of a simple harmonic oscillator is 1.25 eV, what is the frequency of its motion?
When a quantum harmonic oscillator makes a transition from the state to the n state and emits a 450-nm photon, what is its frequency?
Vibrations of the hydrogen molecule can be modeled as a simple harmonic oscillator with the spring constant and mass . (a) What is the vibrational frequency of this molecule? (b) What are the energy and the wavelength of the emitted photon when the molecule makes transition between its third and second excited states?
A particle with mass 0.030 kg oscillates back-and-forth on a spring with frequency 4.0 Hz. At the equilibrium position, it has a speed of 0.60 m/s. If the particle is in a state of definite energy, find its energy quantum number.
Find the expectation value of the square of the position for a quantum harmonic oscillator in the ground state. Note: .
Determine the expectation value of the potential energy for a quantum harmonic oscillator in the ground state. Use this to calculate the expectation value of the kinetic energy.
;
Verify that given by [link] is a solution of Schrӧdinger’s equation for the quantum harmonic oscillator.
Estimate the ground state energy of the quantum harmonic oscillator by Heisenberg’s uncertainty principle. Start by assuming that the product of the uncertainties and is at its minimum. Write in terms of and assume that for the ground state and then write the ground state energy in terms of x . Finally, find the value of x that minimizes the energy and find the minimum of the energy.
proof
A mass of 0.250 kg oscillates on a spring with the force constant 110 N/m. Calculate the ground energy level and the separation between the adjacent energy levels. Express the results in joules and in electron-volts. Are quantum effects important?

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?