| << Chapter < Page | Chapter >> Page > |
where the quantity in parentheses, sandwiched between the wave functions, is called the momentum operator in the x -direction. [The momentum operator in [link] is said to be the position-space representation of the momentum operator.] The momentum operator must act (operate) on the wave function to the right, and then the result must be multiplied by the complex conjugate of the wave function on the left, before integration. The momentum operator in the x -direction is sometimes denoted
Momentum operators for the y - and z -directions are defined similarly. This operator and many others are derived in a more advanced course in modern physics. In some cases, this derivation is relatively simple. For example, the kinetic energy operator is just
Thus, if we seek an expectation value of kinetic energy of a particle in one dimension, two successive ordinary derivatives of the wave function are required before integration.
Expectation-value calculations are often simplified by exploiting the symmetry of wave functions. Symmetric wave functions can be even or odd. An even function is a function that satisfies
In contrast, an odd function is a function that satisfies
An example of even and odd functions is shown in [link] . An even function is symmetric about the y -axis. This function is produced by reflecting for x >0 about the vertical y -axis. By comparison, an odd function is generated by reflecting the function about the y -axis and then about the x -axis. (An odd function is also referred to as an anti-symmetric function .)
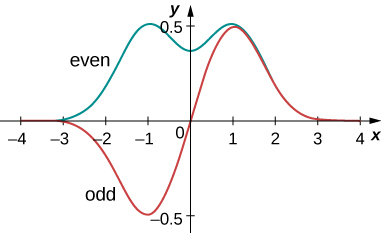
In general, an even function times an even function produces an even function. A simple example of an even function is the product (even times even is even). Similarly, an odd function times an odd function produces an even function, such as x sin x (odd times odd is even). However, an odd function times an even function produces an odd function, such as (odd times even is odd). The integral over all space of an odd function is zero, because the total area of the function above the x -axis cancels the (negative) area below it. As the next example shows, this property of odd functions is very useful.
Find the expectation value of position.

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?