| << Chapter < Page | Chapter >> Page > |
The Galilean transformation nevertheless violates Einstein’s postulates, because the velocity equations state that a pulse of light moving with speed c along the x -axis would travel at speed in the other inertial frame. Specifically, the spherical pulse has radius at time t in the unprimed frame, and also has radius at time in the primed frame. Expressing these relations in Cartesian coordinates gives
The left-hand sides of the two expressions can be set equal because both are zero. Because and we obtain
This cannot be satisfied for nonzero relative velocity v of the two frames if we assume the Galilean transformation results in with
To find the correct set of transformation equations, assume the two coordinate systems S and in [link] . First suppose that an event occurs at in and at in S , as depicted in the figure.
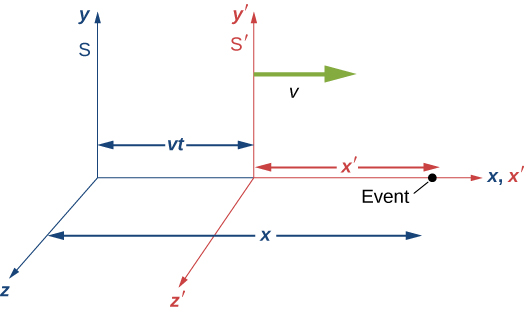
Suppose that at the instant that the origins of the coordinate systems in S and coincide, a flash bulb emits a spherically spreading pulse of light starting from the origin. At time t , an observer in S finds the origin of to be at With the help of a friend in S , the observer also measures the distance from the event to the origin of and finds it to be This follows because we have already shown the postulates of relativity to imply length contraction. Thus the position of the event in S is
and
The postulates of relativity imply that the equation relating distance and time of the spherical wave front:
must apply both in terms of primed and unprimed coordinates, which was shown above to lead to [link] :
We combine this with the equation relating x and to obtain the relation between t and
The equations relating the time and position of the events as seen in S are then
This set of equations, relating the position and time in the two inertial frames, is known as the Lorentz transformation . They are named in honor of H.A. Lorentz (1853–1928), who first proposed them. Interestingly, he justified the transformation on what was eventually discovered to be a fallacious hypothesis. The correct theoretical basis is Einstein’s special theory of relativity.
The reverse transformation expresses the variables in S in terms of those in Simply interchanging the primed and unprimed variables and substituting gives:

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?