| << Chapter < Page | Chapter >> Page > |
The image in a plane mirror has the same size as the object, is upright, and is the same distance behind the mirror as the object is in front of the mirror. A curved mirror , on the other hand, can form images that may be larger or smaller than the object and may form either in front of the mirror or behind it. In general, any curved surface will form an image, although some images make be so distorted as to be unrecognizable (think of fun house mirrors).
Because curved mirrors can create such a rich variety of images, they are used in many optical devices that find many uses. We will concentrate on spherical mirrors for the most part, because they are easier to manufacture than mirrors such as parabolic mirrors and so are more common.
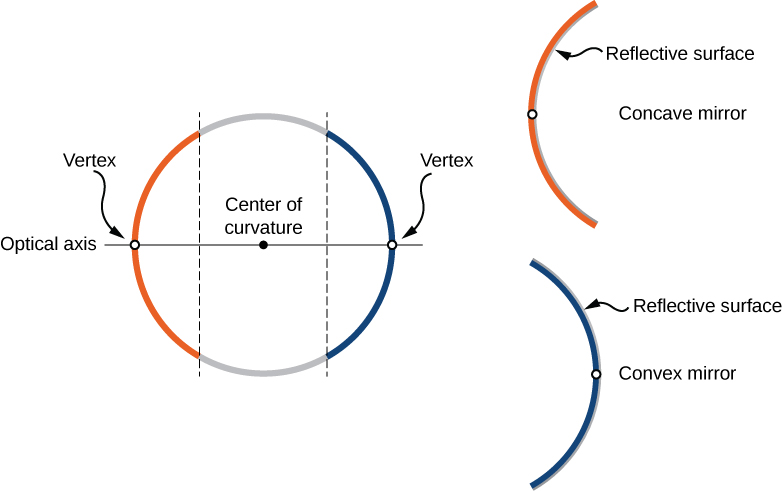
We can define two general types of spherical mirrors. If the reflecting surface is the outer side of the sphere, the mirror is called a convex mirror . If the inside surface is the reflecting surface, it is called a concave mirror .
Symmetry is one of the major hallmarks of many optical devices, including mirrors and lenses. The symmetry axis of such optical elements is often called the principal axis or optical axis . For a spherical mirror, the optical axis passes through the mirror’s center of curvature and the mirror’s vertex , as shown in [link] .
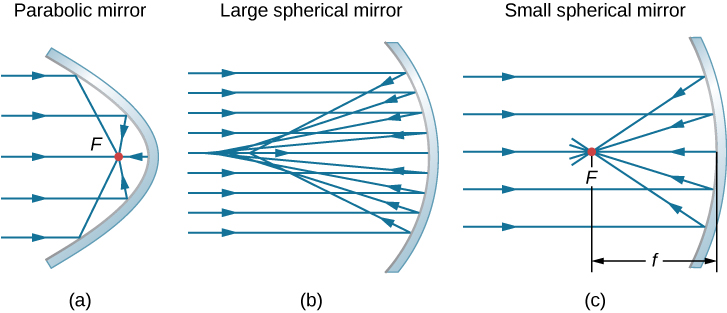
Consider rays that are parallel to the optical axis of a parabolic mirror, as shown in part (a) of [link] . Following the law of reflection, these rays are reflected so that they converge at a point, called the focal point . Part (b) of this figure shows a spherical mirror that is large compared with its radius of curvature. For this mirror, the reflected rays do not cross at the same point, so the mirror does not have a well-defined focal point. This is called spherical aberration and results in a blurred image of an extended object. Part (c) shows a spherical mirror that is small compared to its radius of curvature. This mirror is a good approximation of a parabolic mirror, so rays that arrive parallel to the optical axis are reflected to a well-defined focal point. The distance along the optical axis from the mirror to the focal point is called the focal length of the mirror.

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?