| << Chapter < Page | Chapter >> Page > |
where the direction information is included by using the unit radial vector.
Check Your Understanding Check that the electric fields for the sphere reduce to the correct values for a point charge.
In this case, there is only
A charge distribution has cylindrical symmetry if the charge density depends only upon the distance r from the axis of a cylinder and must not vary along the axis or with direction about the axis. In other words, if your system varies if you rotate it around the axis, or shift it along the axis, you do not have cylindrical symmetry.
[link] shows four situations in which charges are distributed in a cylinder. A uniform charge density in an infinite straight wire has a cylindrical symmetry, and so does an infinitely long cylinder with constant charge density An infinitely long cylinder that has different charge densities along its length, such as a charge density for and for , does not have a usable cylindrical symmetry for this course. Neither does a cylinder in which charge density varies with the direction, such as a charge density for and for . A system with concentric cylindrical shells, each with uniform charge densities, albeit different in different shells, as in [link] (d), does have cylindrical symmetry if they are infinitely long. The infinite length requirement is due to the charge density changing along the axis of a finite cylinder. In real systems, we don’t have infinite cylinders; however, if the cylindrical object is considerably longer than the radius from it that we are interested in, then the approximation of an infinite cylinder becomes useful.
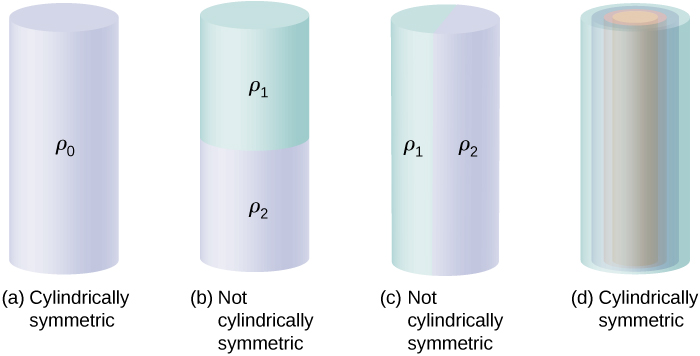
In all cylindrically symmetrical cases, the electric field at any point P must also display cylindrical symmetry.
Cylindrical symmetry: ,
where r is the distance from the axis and is a unit vector directed perpendicularly away from the axis ( [link] ).
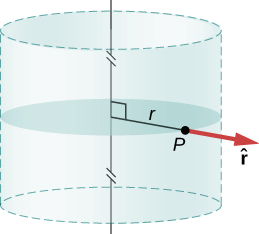
To make use of the direction and functional dependence of the electric field, we choose a closed Gaussian surface in the shape of a cylinder with the same axis as the axis of the charge distribution. The flux through this surface of radius s and height L is easy to compute if we divide our task into two parts: (a) a flux through the flat ends and (b) a flux through the curved surface ( [link] ).

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?