| << Chapter < Page | Chapter >> Page > |
Capacitor networks are usually some combination of series and parallel connections, as shown in [link] . To find the net capacitance of such combinations, we identify parts that contain only series or only parallel connections, and find their equivalent capacitances. We repeat this process until we can determine the equivalent capacitance of the entire network. The following example illustrates this process.
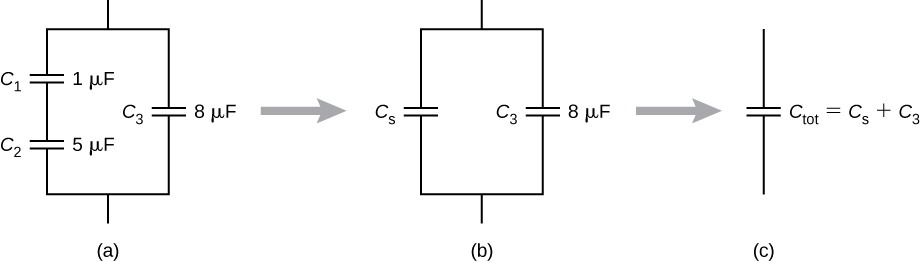
Capacitance is connected in parallel with the third capacitance , so we use [link] to find the equivalent capacitance C of the entire network:

The entire three-capacitor combination is equivalent to two capacitors in series,
Consider the equivalent two-capacitor combination in [link] (b). Since the capacitors are in series, they have the same charge, . Also, the capacitors share the 12.0-V potential difference, so
Now the potential difference across capacitor 1 is
Because capacitors 2 and 3 are connected in parallel, they are at the same potential difference:
Hence, the charges on these two capacitors are, respectively,
Check Your Understanding Determine the net capacitance C of each network of capacitors shown below. Assume that , , , and . Find the charge on each capacitor, assuming there is a potential difference of 12.0 V across each network.
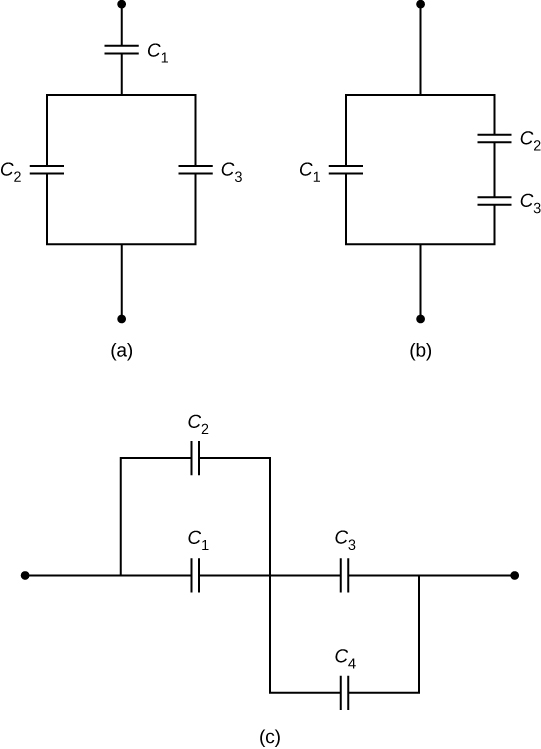
a.
;
b.
;
c.
If you wish to store a large amount of charge in a capacitor bank, would you connect capacitors in series or in parallel? Explain.
What is the maximum capacitance you can get by connecting three capacitors? What is the minimum capacitance?
A 4.00-pF is connected in series with an 8.00-pF capacitor and a 400-V potential difference is applied across the pair. (a) What is the charge on each capacitor? (b) What is the voltage across each capacitor?
a. 1.07 nC; b. 267 V, 133 V
Three capacitors, with capacitances of , and respectively, are connected in parallel. A 500-V potential difference is applied across the combination. Determine the voltage across each capacitor and the charge on each capacitor.
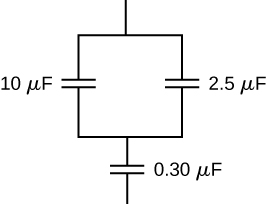
Find the total capacitance of this combination of series and parallel capacitors shown below.
Suppose you need a capacitor bank with a total capacitance of 0.750 F but you have only 1.50-mF capacitors at your disposal. What is the smallest number of capacitors you could connect together to achieve your goal, and how would you connect them?
500 capacitors; connected in parallel
What total capacitances can you make by connecting a and a capacitor?
(series) and (parallel)
Find the equivalent capacitance of the combination of series and parallel capacitors shown below.
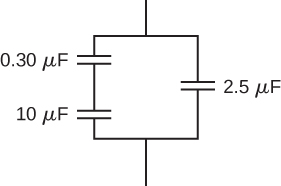
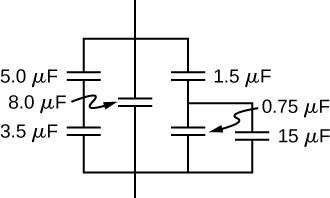
Find the net capacitance of the combination of series and parallel capacitors shown below.
A 40-pF capacitor is charged to a potential difference of 500 V. Its terminals are then connected to those of an uncharged 10-pF capacitor. Calculate: (a) the original charge on the 40-pF capacitor; (b) the charge on each capacitor after the connection is made; and (c) the potential difference across the plates of each capacitor after the connection.
A capacitor and a capacitor are connected in series across a 1.0-kV potential. The charged capacitors are then disconnected from the source and connected to each other with terminals of like sign together. Find the charge on each capacitor and the voltage across each capacitor.
0.89 mC; 1.78 mC; 444 V

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?