| << Chapter < Page | Chapter >> Page > |
Check Your Understanding The resistance between the two conductors of a coaxial cable depends on the resistivity of the material separating the two conductors, the length of the cable and the inner and outer radius of the two conductor. If you are designing a coaxial cable, how does the resistance between the two conductors depend on these variables?
The longer the length, the smaller the resistance. The greater the resistivity, the higher the resistance. The larger the difference between the outer radius and the inner radius, that is, the greater the ratio between the two, the greater the resistance. If you are attempting to maximize the resistance, the choice of the values for these variables will depend on the application. For example, if the cable must be flexible, the choice of materials may be limited.
View this simulation to see how the voltage applied and the resistance of the material the current flows through affects the current through the material. You can visualize the collisions of the electrons and the atoms of the material effect the temperature of the material.
The IR drop across a resistor means that there is a change in potential or voltage across the resistor. Is there any change in current as it passes through a resistor? Explain.
Do impurities in semiconducting materials listed in [link] supply free charges? ( Hint : Examine the range of resistivity for each and determine whether the pure semiconductor has the higher or lower conductivity.)
In carbon, resistivity increases with the amount of impurities, meaning fewer free charges. In silicon and germanium, impurities decrease resistivity, meaning more free electrons.
Does the resistance of an object depend on the path current takes through it? Consider, for example, a rectangular bar—is its resistance the same along its length as across its width?
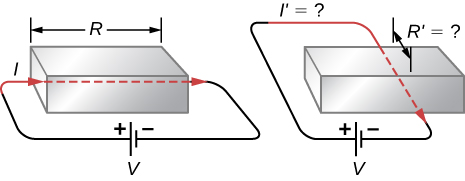
If aluminum and copper wires of the same length have the same resistance, which has the larger diameter? Why?
Copper has a lower resistivity than aluminum, so if length is the same, copper must have the smaller diameter.
What current flows through the bulb of a 3.00-V flashlight when its hot resistance is ?
Calculate the effective resistance of a pocket calculator that has a 1.35-V battery and through which 0.200 mA flows.
How many volts are supplied to operate an indicator light on a DVD player that has a resistance of , given that 25.0 mA passes through it?
What is the resistance of a 20.0-m-long piece of 12-gauge copper wire having a 2.053-mm diameter?
The diameter of 0-gauge copper wire is 8.252 mm. Find the resistance of a 1.00-km length of such wire used for power transmission.
If the 0.100-mm-diameter tungsten filament in a light bulb is to have a resistance of at , how long should it be?
A lead rod has a length of 30.00 cm and a resistance of . What is the radius of the rod?
Find the ratio of the diameter of aluminum to copper wire, if they have the same resistance per unit length (as they might in household wiring).
What current flows through a 2.54-cm-diameter rod of pure silicon that is 20.0 cm long, when is applied to it? (Such a rod may be used to make nuclear-particle detectors, for example.)
(a) To what temperature must you raise a copper wire, originally at , to double its resistance, neglecting any changes in dimensions? (b) Does this happen in household wiring under ordinary circumstances?
a.
;
b. Under normal conditions, no it should not occur.
A resistor made of nichrome wire is used in an application where its resistance cannot change more than 1.00% from its value at . Over what temperature range can it be used?
Of what material is a resistor made if its resistance is 40.0% greater at than at ?
, iron
An electronic device designed to operate at any temperature in the range from to contains pure carbon resistors. By what factor does their resistance increase over this range?
(a) Of what material is a wire made, if it is 25.0 m long with a diameter of 0.100 mm and has a resistance of at ? (b) What is its resistance at
a.
, gold;
b.
Assuming a constant temperature coefficient of resistivity, what is the maximum percent decrease in the resistance of a constantan wire starting at ?
A copper wire has a resistance of at and an iron wire has a resistance of at the same temperature. At what temperature are their resistances equal?

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?