| << Chapter < Page | Chapter >> Page > |
Since is exactly by definition, and because , the force per meter is exactly . This is the basis of the operational definition of the ampere.
The official definition of the ampere is:
One ampere of current through each of two parallel conductors of infinite length, separated by one meter in empty space free of other magnetic fields, causes a force of exactly on each conductor.
Infinite-length straight wires are impractical and so, in practice, a current balance is constructed with coils of wire separated by a few centimeters. Force is measured to determine current. This also provides us with a method for measuring the coulomb. We measure the charge that flows for a current of one ampere in one second. That is, . For both the ampere and the coulomb, the method of measuring force between conductors is the most accurate in practice.
Is the force attractive or repulsive between the hot and neutral lines hung from power poles? Why?
If you have three parallel wires in the same plane, as in [link] , with currents in the outer two running in opposite directions, is it possible for the middle wire to be repelled by both? Attracted by both? Explain.
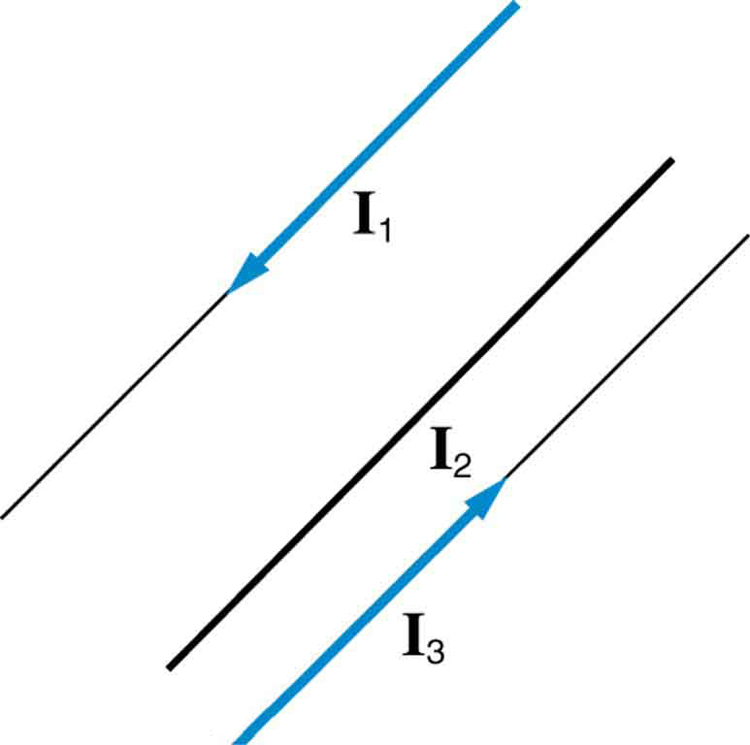
Suppose two long straight wires run perpendicular to one another without touching. Does one exert a net force on the other? If so, what is its direction? Does one exert a net torque on the other? If so, what is its direction? Justify your responses by using the right hand rules.
Use the right hand rules to show that the force between the two loops in [link] is attractive if the currents are in the same direction and repulsive if they are in opposite directions. Is this consistent with like poles of the loops repelling and unlike poles of the loops attracting? Draw sketches to justify your answers.
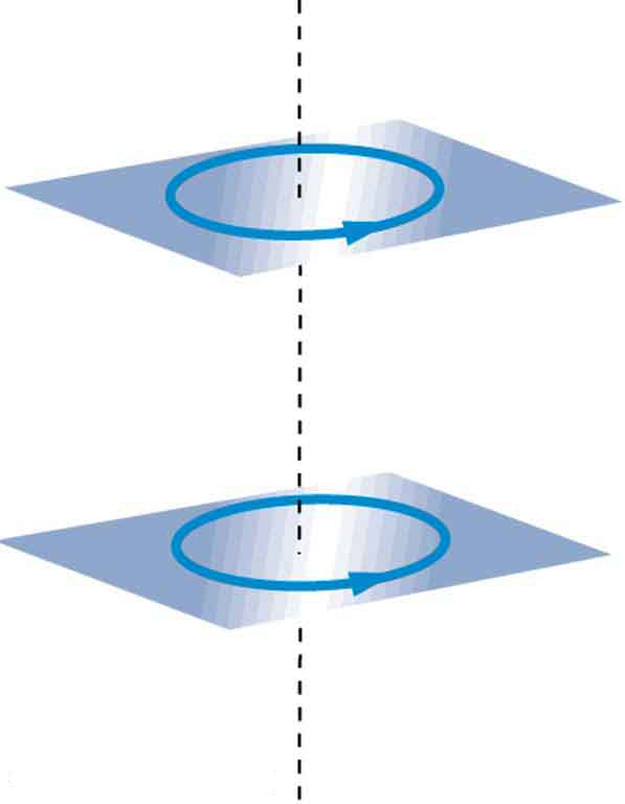
If one of the loops in [link] is tilted slightly relative to the other and their currents are in the same direction, what are the directions of the torques they exert on each other? Does this imply that the poles of the bar magnet-like fields they create will line up with each other if the loops are allowed to rotate?
Electric field lines can be shielded by the Faraday cage effect. Can we have magnetic shielding? Can we have gravitational shielding?
(a) The hot and neutral wires supplying DC power to a light-rail commuter train carry 800 A and are separated by 75.0 cm. What is the magnitude and direction of the force between 50.0 m of these wires? (b) Discuss the practical consequences of this force, if any.
(a) 8.53 N, repulsive
(b) This forceis repulsiveand thereforethere isnever arisk thatthe twowires willtouch andshort circuit.
The force per meter between the two wires of a jumper cable being used to start a stalled car is 0.225 N/m. (a) What is the current in the wires, given they are separated by 2.00 cm? (b) Is the force attractive or repulsive?
A 2.50-m segment of wire supplying current to the motor of a submerged submarine carries 1000 A and feels a 4.00-N repulsive force from a parallel wire 5.00 cm away. What is the direction and magnitude of the current in the other wire?
400 A in the opposite direction
The wire carrying 400 A to the motor of a commuter train feels an attractive force of due to a parallel wire carrying 5.00 A to a headlight. (a) How far apart are the wires? (b) Are the currents in the same direction?
An AC appliance cord has its hot and neutral wires separated by 3.00 mm and carries a 5.00-A current. (a) What is the average force per meter between the wires in the cord? (b) What is the maximum force per meter between the wires? (c) Are the forces attractive or repulsive? (d) Do appliance cords need any special design features to compensate for these forces?
(a)
(b)
(c) Repulsive
(d) No, these are very small forces
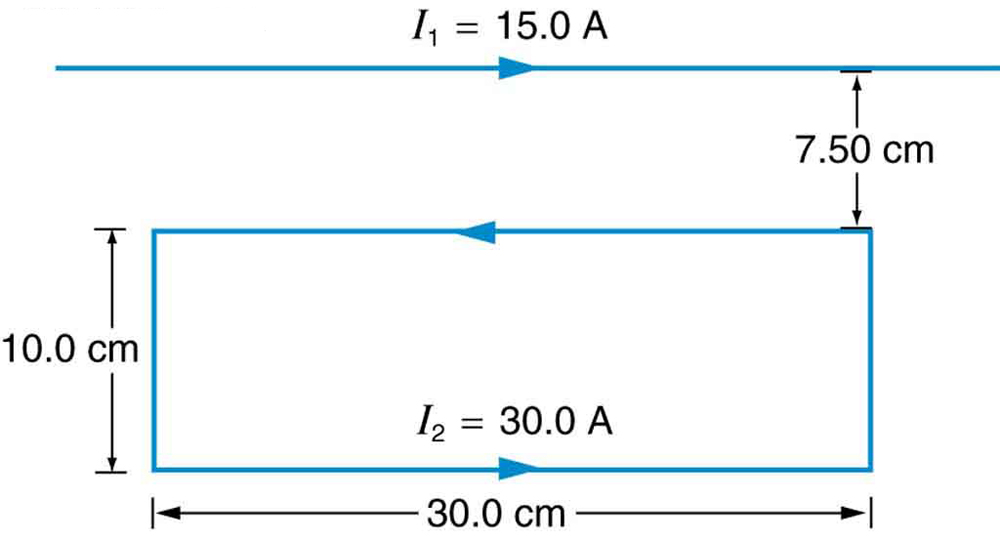
[link] shows a long straight wire near a rectangular current loop. What is the direction and magnitude of the total force on the loop?
Find the direction and magnitude of the force that each wire experiences in [link] (a) by, using vector addition.
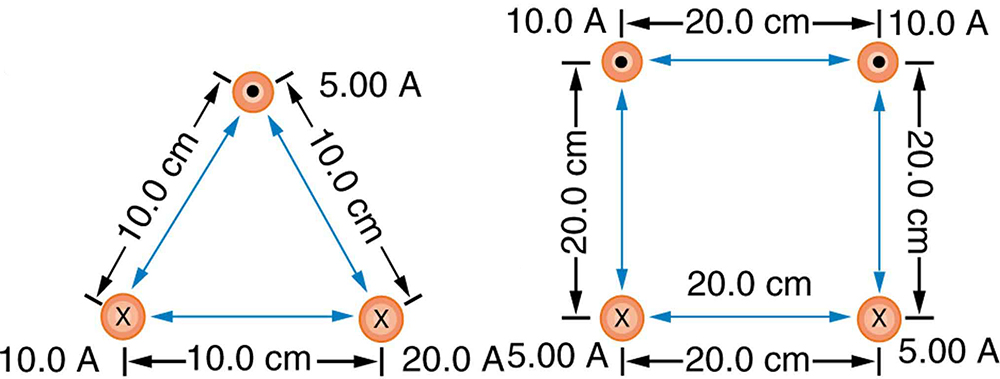
(a) Top wire: s, to left of up
(b) Lower left wire: , down from right
(c) Lower right wire: , down from left
Find the direction and magnitude of the force that each wire experiences in [link] (b), using vector addition.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?