| << Chapter < Page | Chapter >> Page > |
Check Your Understanding What are the equipotential surfaces for an infinite line charge?
infinite cylinders of constant radius, with the line charge as the axis
In [link] with a point charge, we found that the equipotential surfaces were in the form of spheres, with the point charge at the center. Given that a conducting sphere in electrostatic equilibrium is a spherical equipotential surface, we should expect that we could replace one of the surfaces in [link] with a conducting sphere and have an identical solution outside the sphere. Inside will be rather different, however.
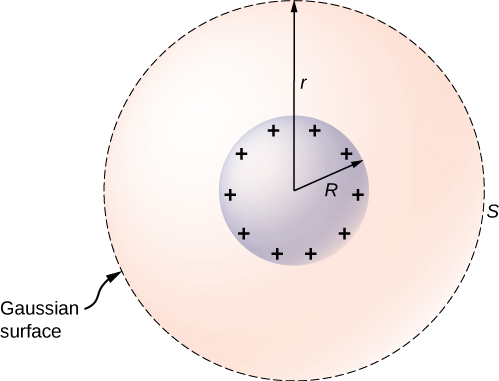
To investigate this, consider the isolated conducting sphere of [link] that has a radius R and an excess charge q . To find the electric field both inside and outside the sphere, note that the sphere is isolated, so its surface change distribution and the electric field of that distribution are spherically symmetric. We can therefore represent the field as To calculate E(r) , we apply Gauss’s law over a closed spherical surface S of radius r that is concentric with the conducting sphere. Since r is constant and on the sphere,
For , S is within the conductor, so recall from our previous study of Gauss’s law that and Gauss’s law gives , as expected inside a conductor at equilibrium. If , S encloses the conductor so From Gauss’s law,
The electric field of the sphere may therefore be written as
As expected, in the region the electric field due to a charge q placed on an isolated conducting sphere of radius R is identical to the electric field of a point charge q located at the center of the sphere.
To find the electric potential inside and outside the sphere, note that for the potential must be the same as that of an isolated point charge q located at ,
simply due to the similarity of the electric field.
For so V ( r ) is constant in this region. Since
We will use this result to show that
for two conducting spheres of radii , with surface charge densities respectively, that are connected by a thin wire, as shown in [link] . The spheres are sufficiently separated so that each can be treated as if it were isolated (aside from the wire). Note that the connection by the wire means that this entire system must be an equipotential.

We have just seen that the electrical potential at the surface of an isolated, charged conducting sphere of radius R is
Now, the spheres are connected by a conductor and are therefore at the same potential; hence
and
The net charge on a conducting sphere and its surface charge density are related by Substituting this equation into the previous one, we find
Obviously, two spheres connected by a thin wire do not constitute a typical conductor with a variable radius of curvature. Nevertheless, this result does at least provide a qualitative idea of how charge density varies over the surface of a conductor. The equation indicates that where the radius of curvature is large (points B and D in [link] ), and E are small.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?