| << Chapter < Page | Chapter >> Page > |
As an example, let us determine the net entropy change of a reversible engine while it undergoes a single Carnot cycle. In the adiabatic steps 2 and 4 of the cycle shown in [link] , no heat exchange takes place, so In step 1, the engine absorbs heat at a temperature so its entropy change is Similarly, in step 3, The net entropy change of the engine in one cycle of operation is then
However, we know that for a Carnot engine,
so
There is no net change in the entropy of the Carnot engine over a complete cycle. Although this result was obtained for a particular case, its validity can be shown to be far more general: There is no net change in the entropy of a system undergoing any complete reversible cyclic process. Mathematically, we write this statement as
where represents the integral over a closed reversible path .
We can use [link] to show that the entropy change of a system undergoing a reversible process between two given states is path independent. An arbitrary, closed path for a reversible cycle that passes through the states A and B is shown in [link] . From [link] , for this closed path. We may split this integral into two segments, one along I, which leads from A to B , the other along II, which leads from B to A . Then
Since the process is reversible,
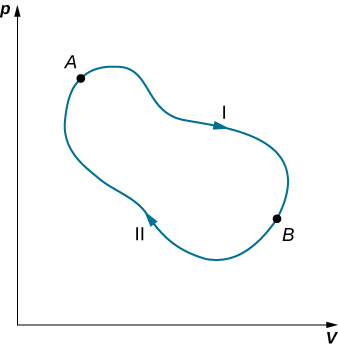
Hence, the entropy change in going from A to B is the same for paths I and II. Since paths I and II are arbitrary, reversible paths, the entropy change in a transition between two equilibrium states is the same for all the reversible processes joining these states. Entropy, like internal energy, is therefore a state function.
What happens if the process is irreversible? When the process is irreversible, we expect the entropy of a closed system, or the system and its environment (the universe), to increase. Therefore we can rewrite this expression as
where S is the total entropy of the closed system or the entire universe, and the equal sign is for a reversible process. The fact is the entropy statement of the second law of thermodynamics :
The entropy of a closed system and the entire universe never decreases.
We can show that this statement is consistent with the Kelvin statement, the Clausius statement, and the Carnot principle.
From the definition of heat capacity, an infinitesimal exchange dQ for the object is related to its temperature change dT by
Substituting this dQ into the expression for , we obtain the entropy change of the object as it is cooled at constant pressure from
Note that here because In other words, the object has lost some entropy. But if we count whatever is used to remove the heat from the object, we would still end up with because the process is irreversible.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?