| << Chapter < Page | Chapter >> Page > |
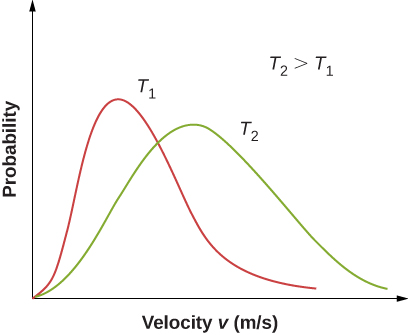
[link] shows that the curve is shifted to higher speeds at higher temperatures, with a broader range of speeds.
With only a relatively small number of molecules, the distribution of speeds fluctuates around the Maxwell-Boltzmann distribution. However, you can view this simulation to see the essential features that more massive molecules move slower and have a narrower distribution. Use the set-up “2 Gases, Random Speeds”. Note the display at the bottom comparing histograms of the speed distributions with the theoretical curves.
We can use a probability distribution to calculate average values by multiplying the distribution function by the quantity to be averaged and integrating the product over all possible speeds. (This is analogous to calculating averages of discrete distributions, where you multiply each value by the number of times it occurs, add the results, and divide by the number of values. The integral is analogous to the first two steps, and the normalization is analogous to dividing by the number of values.) Thus the average velocity is
Similarly,
as in Pressure, Temperature, and RMS Speed . The most probable speed , also called the peak speed is the speed at the peak of the velocity distribution. (In statistics it would be called the mode.) It is less than the rms speed The most probable speed can be calculated by the more familiar method of setting the derivative of the distribution function, with respect to v , equal to 0. The result is
which is less than In fact, the rms speed is greater than both the most probable speed and the average speed.
The peak speed provides a sometimes more convenient way to write the Maxwell-Boltzmann distribution function:
In the factor , it is easy to recognize the translational kinetic energy. Thus, that expression is equal to The distribution f ( v ) can be transformed into a kinetic energy distribution by requiring that Boltzmann showed that the resulting formula is much more generally applicable if we replace the kinetic energy of translation with the total mechanical energy E . Boltzmann’s result is
The first part of this equation, with the negative exponential, is the usual way to write it. We give the second part only to remark that in the denominator is ubiquitous in quantum as well as classical statistical mechanics.
Step 1. Examine the situation to determine that it relates to the distribution of molecular speeds.
Step 2. Make a list of what quantities are given or can be inferred from the problem as stated (identify the known quantities).
Step 3. Identify exactly what needs to be determined in the problem (identify the unknown quantities). A written list is useful.
Step 4. Convert known values into proper SI units (K for temperature, Pa for pressure, for volume, molecules for N , and moles for n ). In many cases, though, using R and the molar mass will be more convenient than using and the molecular mass.
Step 5. Determine whether you need the distribution function for velocity or the one for energy, and whether you are using a formula for one of the characteristic speeds (average, most probably, or rms), finding a ratio of values of the distribution function, or approximating an integral.
Step 6. Solve the appropriate equation for the ideal gas law for the quantity to be determined (the unknown quantity). Note that if you are taking a ratio of values of the distribution function, the normalization factors divide out. Or if approximating an integral, use the method asked for in the problem.
Step 7. Substitute the known quantities, along with their units, into the appropriate equation and obtain numerical solutions complete with units.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?