| << Chapter < Page | Chapter >> Page > |
In the RLC series circuit of [link] , the current amplitude is, from [link] ,
If we can vary the frequency of the ac generator while keeping the amplitude of its output voltage constant, then the current changes accordingly. A plot of versus is shown in [link] .
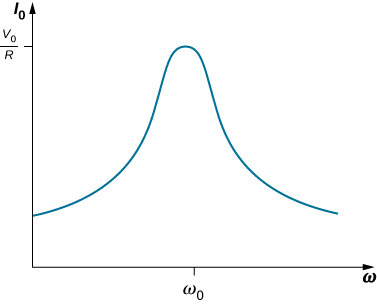
In Oscillations , we encountered a similar graph where the amplitude of a damped harmonic oscillator was plotted against the angular frequency of a sinusoidal driving force (see Forced Oscillations ). This similarity is more than just a coincidence, as shown earlier by the application of Kirchhoff’s loop rule to the circuit of [link] . This yields
or
where we substituted dq (t)/ dt for i (t). A comparison of [link] and, from Oscillations , Damped Oscillations for damped harmonic motion clearly demonstrates that the driven RLC series circuit is the electrical analog of the driven damped harmonic oscillator.
The resonant frequency of the RLC circuit is the frequency at which the amplitude of the current is a maximum and the circuit would oscillate if not driven by a voltage source. By inspection, this corresponds to the angular frequency at which the impedance Z in [link] is a minimum, or when
and
This is the resonant angular frequency of the circuit. Substituting into [link] , [link] , and [link] , we find that at resonance,
Therefore, at resonance, an RLC circuit is purely resistive, with the applied emf and current in phase.
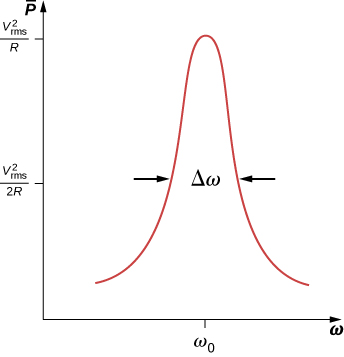
What happens to the power at resonance? [link] tells us how the average power transferred from an ac generator to the RLC combination varies with frequency. In addition, reaches a maximum when Z , which depends on the frequency, is a minimum, that is, when Thus, at resonance, the average power output of the source in an RLC series circuit is a maximum. From [link] , this maximum is
[link] is a typical plot of versus in the region of maximum power output. The bandwidth of the resonance peak is defined as the range of angular frequencies over which the average power is greater than one-half the maximum value of The sharpness of the peak is described by a dimensionless quantity known as the quality factor Q of the circuit. By definition,
where is the resonant angular frequency. A high Q indicates a sharp resonance peak. We can give Q in terms of the circuit parameters as
Resonant circuits are commonly used to pass or reject selected frequency ranges. This is done by adjusting the value of one of the elements and hence “tuning” the circuit to a particular resonant frequency. For example, in radios, the receiver is tuned to the desired station by adjusting the resonant frequency of its circuitry to match the frequency of the station. If the tuning circuit has a high Q , it will have a small bandwidth, so signals from other stations at frequencies even slightly different from the resonant frequency encounter a high impedance and are not passed by the circuit. Cell phones work in a similar fashion, communicating with signals of around 1 GHz that are tuned by an inductor-capacitor circuit. One of the most common applications of capacitors is their use in ac-timing circuits, based on attaining a resonant frequency. A metal detector also uses a shift in resonance frequency in detecting metals ( [link] ).

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?