| << Chapter < Page | Chapter >> Page > |
(a) An exterior wall of a house is 3 m tall and 10 m wide. It consists of a layer of drywall with an R factor of 0.56, a layer 3.5 inches thick filled with fiberglass batts, and a layer of insulated siding with an R factor of 2.6. The wall is built so well that there are no leaks of air through it. When the inside of the wall is at and the outside is at , what is the rate of heat flow through the wall? (b) More realistically, the 3.5-inch space also contains 2-by-4 studs—wooden boards 1.5 inches by 3.5 inches oriented so that 3.5-inch dimension extends from the drywall to the siding. They are “on 16-inch centers,” that is, the centers of the studs are 16 inches apart. What is the heat current in this situation? Don’t worry about one stud more or less.
For the human body, what is the rate of heat transfer by conduction through the body’s tissue with the following conditions: the tissue thickness is 3.00 cm, the difference in temperature is , and the skin area is . How does this compare with the average heat transfer rate to the body resulting from an energy intake of about 2400 kcal per day? (No exercise is included.)
The rate of heat transfer by conduction is 20.0 W. On a daily basis, this is 1,728 kJ/day. Daily food intake is . So only 17.2% of energy intake goes as heat transfer by conduction to the environment at this .
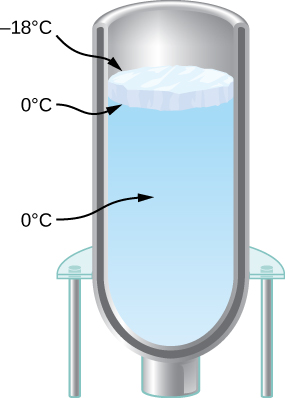
You have a Dewar flask (a laboratory vacuum flask) that has an open top and straight sides, as shown below. You fill it with water and put it into the freezer. It is effectively a perfect insulator, blocking all heat transfer, except on the top. After a time, ice forms on the surface of the water. The liquid water and the bottom surface of the ice, in contact with the liquid water, are at . The top surface of the ice is at the same temperature as the air in the freezer, Set the rate of heat flow through the ice equal to the rate of loss of heat of fusion as the water freezes. When the ice layer is 0.700 cm thick, find the rate in m/s at which the ice is thickening.
An infrared heater for a sauna has a surface area of and an emissivity of 0.84. What temperature must it run at if the required power is 360 W? Neglect the temperature of the environment.
620 K
(a) Determine the power of radiation from the Sun by noting that the intensity of the radiation at the distance of Earth is . Hint: That intensity will be found everywhere on a spherical surface with radius equal to that of Earth’s orbit. (b) Assuming that the Sun’s temperature is 5780 K and that its emissivity is 1, find its radius.
A pendulum is made of a rod of length L and negligible mass, but capable of thermal expansion, and a weight of negligible size. (a) Show that when the temperature increases by dT , the period of the pendulum increases by a fraction . (b) A clock controlled by a brass pendulum keeps time correctly at . If the room temperature is , does the clock run faster or slower? What is its error in seconds per day?
Denoting the period by
P , we know
When the temperature increases by
dT , the length increases by
. Then the new length is a.
by the binomial expansion. b. The clock runs slower, as its new period is 1.00019 s. It loses 16.4 s per day.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?