| << Chapter < Page | Chapter >> Page > |
The relationship between volume and temperature is given by , where is the coefficient of volume expansion . As you can show in [link] , . This equation is usually written as
Note that the values of in [link] are equal to except for rounding.
Volume expansion is defined for liquids, but linear and area expansion are not, as a liquid’s changes in linear dimensions and area depend on the shape of its container. Thus, [link] shows liquids’ values of but not .
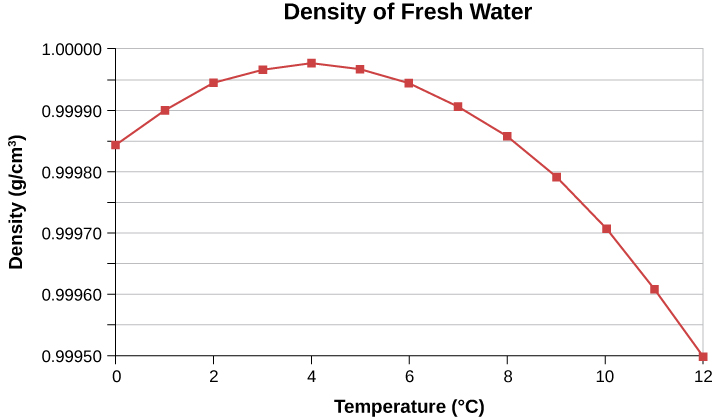
In general, objects expand with increasing temperature. Water is the most important exception to this rule. Water does expand with increasing temperature (its density decreases ) at temperatures greater than . However, it is densest at and expands with decreasing temperature between and ( ), as shown in [link] . A striking effect of this phenomenon is the freezing of water in a pond. When water near the surface cools down to it is denser than the remaining water and thus sinks to the bottom. This “turnover” leaves a layer of warmer water near the surface, which is then cooled. However, if the temperature in the surface layer drops below , that water is less dense than the water below, and thus stays near the top. As a result, the pond surface can freeze over. The layer of ice insulates the liquid water below it from low air temperatures. Fish and other aquatic life can survive in water beneath ice, due to this unusual characteristic of water.
Alternatively, we can combine these three equations into a single equation. (Note that the original volumes are equal.)
If you try to cap the tank tightly to prevent overflow, you will find that it leaks anyway, either around the cap or by bursting the tank. Tightly constricting the expanding gas is equivalent to compressing it, and both liquids and solids resist compression with extremely large forces. To avoid rupturing rigid containers, these containers have air gaps, which allow them to expand and contract without stressing them.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?