| << Chapter < Page | Chapter >> Page > |
Let us consider a tennis ball (mass = 0,1 kg) that is dropped at an initial velocity of 5 m s and bounces back at a final velocity of 3 m s . As the ball approaches the floor it has a momentum that we call the momentum before the collision. When it moves away from the floor it has a different momentum called the momentum after the collision. The bounce on the floor can be thought of as a collision taking place where the floor exerts a force on the tennis ball to change its momentum.
The momentum before the bounce can be calculated as follows:
Because momentum and velocity are vectors, we have to choose a direction as positive. For this example we choose the initial direction of motion as positive, in other words, downwards is positive.
When the tennis ball bounces back it changes direction. The final velocity will thus have a negative value. The momentum after the bounce can be calculated as follows:
Now let us look at what happens to the momentum of the tennis ball. The momentum changes during this bounce. We can calculate the change in momentum as follows:
Again we have to choose a direction as positive and we will stick to our initial choice as downwards is positive. This means that the final momentum will have a negative number.
You will notice that this number is bigger than the previous momenta calculated. This is should be the case as the ball needed to be stopped and then given momentum to bounce back.
A rubber ball of mass 0,8 kg is dropped and strikes the floor with an initial velocity of 6 m s . It bounces back with a final velocity of 4 m s . Calculate the change in the momentum of the rubber ball caused by the floor.
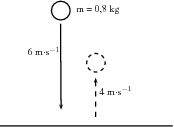
The question explicitly gives
all in the correct units.
We are asked to calculate the change in momentum of the ball,
We have everything we need to find . Since the initial momentum is directed downwards and the final momentum is in the upward direction, we can use the algebraic method of subtraction discussed in the vectors chapter.
Let us choose down as the positive direction.
You have learned about Newton's Second Law of motion earlier in this chapter. Newton's Second Law describes the relationship between the motion of an object and the net force on the object. We said that the motion of an object, and therefore its momentum, can only change when a resultant force is acting on it. We can therefore say that because a net force causes an object to move, it also causes its momentum to change. We can now define Newton's Second Law of motion in terms of momentum.
The net or resultant force acting on an object is equal to the rate of change of momentum.
Mathematically, Newton's Second Law can be stated as:

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 11 physical science' conversation and receive update notifications?