| << Chapter < Page | Chapter >> Page > |
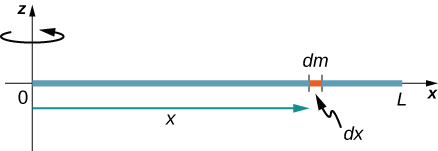
Note the rotational inertia of the rod about its endpoint is larger than the rotational inertia about its center (consistent with the barbell example) by a factor of four.
The similarity between the process of finding the moment of inertia of a rod about an axis through its middle and about an axis through its end is striking, and suggests that there might be a simpler method for determining the moment of inertia for a rod about any axis parallel to the axis through the center of mass. Such an axis is called a parallel axis . There is a theorem for this, called the parallel-axis theorem , which we state here but do not derive in this text.
Let m be the mass of an object and let d be the distance from an axis through the object’s center of mass to a new axis. Then we have
Let’s apply this to the rod examples solved above:
This result agrees with our more lengthy calculation from above. This is a useful equation that we apply in some of the examples and problems.
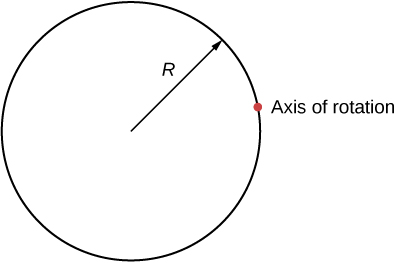
Check Your Understanding What is the moment of inertia of a cylinder of radius R and mass m about an axis through a point on the surface, as shown below?
Integrating to find the moment of inertia of a two-dimensional object is a little bit trickier, but one shape is commonly done at this level of study—a uniform thin disk about an axis through its center ( [link] ).
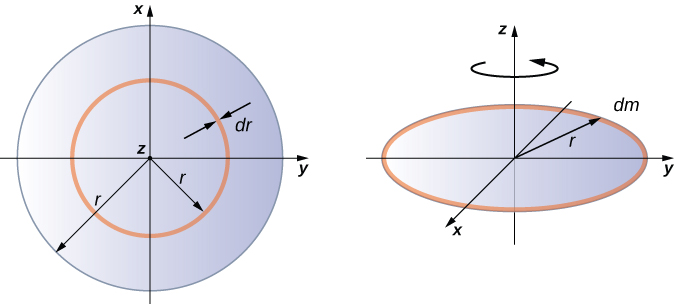
Since the disk is thin, we can take the mass as distributed entirely in the xy -plane. We again start with the relationship for the surface mass density , which is the mass per unit surface area. Since it is uniform, the surface mass density is constant:
Now we use a simplification for the area. The area can be thought of as made up of a series of thin rings, where each ring is a mass increment dm of radius r equidistanct from the axis, as shown in part (b) of the figure. The infinitesimal area of each ring dA is therefore given by the length of each ring ( ) times the infinitesimmal width of each ring dr :
The full area of the disk is then made up from adding all the thin rings with a radius range from 0 to R . This radius range then becomes our limits of integration for dr , that is, we integrate from to . Putting this all together, we have
Note that this agrees with the value given in [link] .
Now consider a compound object such as that in [link] , which depicts a thin disk at the end of a thin rod. This cannot be easily integrated to find the moment of inertia because it is not a uniformly shaped object. However, if we go back to the initial definition of moment of inertia as a summation, we can reason that a compound object’s moment of inertia can be found from the sum of each part of the object:

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?